
分析 畫出函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象,要使直線y=kx+$\frac{1}{2}$(k>0)與函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象有且只有2個交點,只需直線經過(2,3)和經過(2,$\frac{1}{2}$)之間.
解答 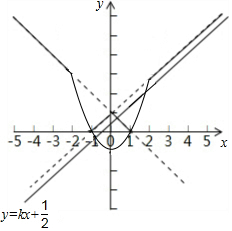 解:函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象如圖所示
解:函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象如圖所示
∵直線y=kx+$\frac{1}{2}$(k>0)與函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象有且只有2個交點,
當直線y=kx+$\frac{1}{2}$(k>0)經過點(2,3)時,則3=2k+$\frac{1}{2}$,
解得k=$\frac{5}{4}$,
當直線y=kx+$\frac{1}{2}$(k>0)經過點(-1,0)時,k=$\frac{1}{2}$,
當k=1時,平行于y=x+1,與函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象也有且僅有兩個交點;
∴直線y=kx+$\frac{1}{2}$(k>0)與函數y=$\left\{\begin{array}{l}{-x+1(x≤2)}\\{{x}^{2}+1(-2<x<2)}\\{x+1(x≥2)}\end{array}\right.$的圖象有且只有2個交點,則k的取值為$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
故答案為$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
點評 本題考查了一次函數的性質以及一次函數的圖象和二次函數的圖象,數形結合思想的應用是解題的關鍵.


 名題訓練系列答案
名題訓練系列答案 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:選擇題
| 時間(s) | 0 | 5 | 10 | 15 |
| 食用油溫度(℃) | 20 | 35 | 50 | 65 |
| A. | 85℃ | B. | 120℃ | C. | 150℃ | D. | 170℃ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,半徑為5的⊙P與y軸交于點M(0,-4),N(0,-10),函數y=$\frac{k}{x}$(x<0)的圖象過點P,則k的值為( )
如圖,半徑為5的⊙P與y軸交于點M(0,-4),N(0,-10),函數y=$\frac{k}{x}$(x<0)的圖象過點P,則k的值為( )| A. | -28 | B. | -20 | C. | 28 | D. | 26 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
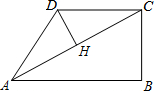 在四邊形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,點H為垂足,設AB=x,AD=y,則y關于x的函數關系用圖象大致可以表示為( )
在四邊形ABCD中,∠B=90°,AC=4,AB∥CD,DH垂直平分AC,點H為垂足,設AB=x,AD=y,則y關于x的函數關系用圖象大致可以表示為( )| A. | 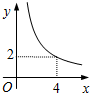 | B. | 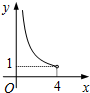 | C. | 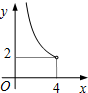 | D. | 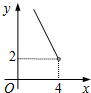 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
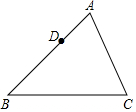 如圖,已知銳角△ABC,點D是AB邊上的一定點,請用尺規在AC邊上求作一點E,使△ADE與△ABC相似.(作出符合題意的一個點即可,保留作圖痕跡,不寫作法.)
如圖,已知銳角△ABC,點D是AB邊上的一定點,請用尺規在AC邊上求作一點E,使△ADE與△ABC相似.(作出符合題意的一個點即可,保留作圖痕跡,不寫作法.)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com