
分析 結合x的范圍畫出函數y=Z{x+2,x2}的圖象,由直線y=-x+m與該函數圖象只有兩個交點且,判斷直線的位置得①直線y=y=-x+m經過點(-1,1)時可以求出m;②直線y=y=-x+m與函數y=x2相切時,可以求出m.
解答 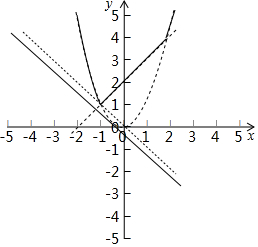 解:根據題意,x2<x+2,即x2-x-2<0,
解:根據題意,x2<x+2,即x2-x-2<0,
解得:-1<x<2,
故當-1<x<2時,y=x+2;
當x≤-1或x≥2時,y=x2;
函數圖象如下:
由圖象可知,∵直線y=-x+m與函數y=Z{x+2,x2}的圖象有且只有2個交點,且k<0,
①直線y=-x+m經過點(-1,1)時,1=1+m,m=0,此時直線y=-x與函數y=Z{x+2,x2}的圖象有且只有2個交點.
②直線y=-x+m與函數y=x2相切時,由$\left\{\begin{array}{l}{y={x}^{2}}\\{y=-x+m}\end{array}\right.$消去y得x2+x-m=0,∵△=0,
∴1+4m=0,
∴m=-$\frac{1}{4}$,此時直線y=-x-$\frac{1}{4}$與函數y=Z{x+2,x2}的圖象有且只有2個交點.
③由圖象知,當m>0時,直線y=-x-$\frac{1}{4}$與函數y=Z{x+2,x2}的圖象有且只有2個交點.
綜上,m≥0或-$\frac{1}{4}$時,一次函數y=-x+m與函數y=Z{x+2,x2}的圖象有且只有2個交點,
故答案為:m≥0或-$\frac{1}{4}$.
點評 本題主要考查二次函數與一元一次不等式間的關系,根據題意判斷直線的位置是關鍵,學會用轉化的思想解決問題,屬于中考填空題中的壓軸題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
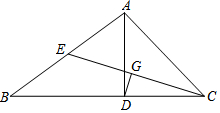 已知:如圖,在△ABC中,AD是BC邊上的高,∠B=30°,∠ACB=45°,CE是AB邊上的中線.
已知:如圖,在△ABC中,AD是BC邊上的高,∠B=30°,∠ACB=45°,CE是AB邊上的中線.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
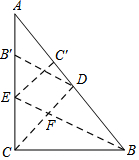 如圖,在 Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折疊,使點B落在CA邊上的B'處,展開后,再沿BE折疊,使點C落在BA邊上的C'處,CD與BE交于點F.
如圖,在 Rt△ABC中,∠ACB=90°,BC=3,AC=4,沿CD折疊,使點B落在CA邊上的B'處,展開后,再沿BE折疊,使點C落在BA邊上的C'處,CD與BE交于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 4,5,6 | B. | 1.5,2,2.5 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com