
 如圖,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,點M,N分別為AD,AC上的動點,則CM+MN的最小值是2.4.
如圖,在△ABC中,AB=5,BC=3,CA=4,AD平分∠BAC,點M,N分別為AD,AC上的動點,則CM+MN的最小值是2.4. 分析 取點N關于AD的對稱點E,由軸對稱圖形的性質可知MN=ME,從而得到CM+MN=CM+ME,當點C、M、E在一條直線上且CE⊥AB時,CM+MN有最小值,然后證明△ABC為直角三角形,最后利用面積法求得CE的值即可.
解答 解:取點N關于AD的對稱點E.
∵AD平分∠BAC,
∴點E在AB上.
∵點N與點D關于AD對稱,
∴MN=ME.
∴CM+MN=CM+ME.
當CE⊥AB時,CE有最小值,即CM+MN有最小值.
在△ABC中,AB=5,BC=3,CA=4,
∴△ABC為直角三角形.
∴AC•BC=AB•CE,即5CE=3×4,解得CE=2.4.
故答案為:2.4.
點評 本題主要考查的是軸對稱-路徑最短問題,解答本題主要應用了軸對稱圖形的性質、垂線段最短的性質,將CM+MN轉化為CE的長是解題的關鍵.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:初中數學 來源: 題型:解答題
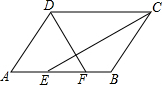 如圖,在?ABCD中,∠ADC、∠DCB的平分線分別交邊AB于點F,E.
如圖,在?ABCD中,∠ADC、∠DCB的平分線分別交邊AB于點F,E.查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:選擇題

| A. | 20厘米 | B. | 8π厘米 | C. | 7π厘米 | D. | 5π厘米 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
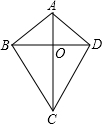 如圖,四邊形ABCD的對角線AC、BD相交于點O,△ABO≌△ADO,下列結論:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正確結論的個數有( )
如圖,四邊形ABCD的對角線AC、BD相交于點O,△ABO≌△ADO,下列結論:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正確結論的個數有( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com