
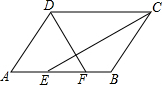
 如圖,在?ABCD中,∠ADC、∠DCB的平分線分別交邊AB于點F,E.
如圖,在?ABCD中,∠ADC、∠DCB的平分線分別交邊AB于點F,E.分析 (1)根據角平分線的定義以及平行線的性質,得出∠AFD=∠ADF,進而得到AF=AD=BC=3,同理可得,BE=CB=3,最后根據EF=BE+AF-AB進行計算即可;
(2)根據角平分線的定義以及平行線的性質,得出∠BCE=∠BEC,進而得到BC=BE=3,再根據EF=1,求得BF=3-1=2,同理可得,AD=AF=3,最后根據AB=AF+BF進行計算即可;
(3)根據角平分線的定義以及平行線的性質,∠AFD=∠ADF,進而得出AF=AD=BC=a,同理可得,BE=CB=a,得出AE=AB-BE=b-a,最后得到EF=|AF-AE|=|a-b+a|=|2a-b|.
解答  解:(1)∵DF平分∠ADC,
解:(1)∵DF平分∠ADC,
∴∠ADF=∠CDF,
又∵AB∥CD,
∴∠AFD=∠CDF,
∴∠AFD=∠ADF,
∴AF=AD=BC=3,
同理可得,BE=CB=3,
∴EF=BE+AF-AB=3+3-5=1;
(2)∵CE平分∠DCB,
∴∠DCE=∠BCE,
又∵AB∥CD,
∴∠DCE=∠BEC,
∴∠BCE=∠BEC,
∴BC=BE=3,
∵EF=1,
∴BF=3-1=2,
同理可得,AD=AF=3,
∴AB=AF+BF=3+2=5;
(3)∵DF平分∠ADC,
∴∠ADF=∠CDF,
又∵AB∥CD,
∴∠AFD=∠CDF,
∴∠AFD=∠ADF,
∴AF=AD=BC=a,
同理可得,BE=CB=a,
∴AE=AB-BE=b-a,
∴EF=|AF-AE|=|a-b+a|=|2a-b|.
點評 此題主要考查了角平分線的定義、平行四邊形的性質、平行線的性質等知識的綜合應用,解決問題的關鍵是找出線段之間的關系:EF=BE+CF-BC.


科目:初中數學 來源: 題型:選擇題
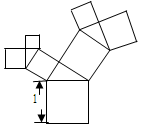 有一個面積為1的正方形,經過一次“生長”后,在他的左右肩上生出兩個小正方形,其中,三個正方形圍成的三角形是直角三角形,再經過一次“生長”后,變成了該圖,如果繼續“生長”下去,它將變得“枝繁葉茂”,請你算出“生長”了2016次后形成的圖形中所有的正方形的面積和是( )
有一個面積為1的正方形,經過一次“生長”后,在他的左右肩上生出兩個小正方形,其中,三個正方形圍成的三角形是直角三角形,再經過一次“生長”后,變成了該圖,如果繼續“生長”下去,它將變得“枝繁葉茂”,請你算出“生長”了2016次后形成的圖形中所有的正方形的面積和是( )| A. | 1 | B. | 2015 | C. | 2016 | D. | 2017 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
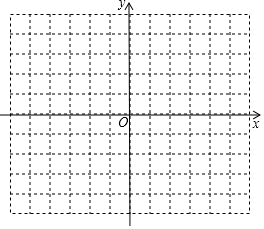 如圖,在平面直角坐標系中,圖中小正方形的邊長均為1,已知△ABC三個頂點的坐標分別為A(-2,2),B(-4,0),C(-4,-4).
如圖,在平面直角坐標系中,圖中小正方形的邊長均為1,已知△ABC三個頂點的坐標分別為A(-2,2),B(-4,0),C(-4,-4).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
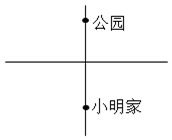 如圖,小明周末到公園走到十字路口處,記不清前面哪條路通往公園,那么他能一次選對路的概率是( )
如圖,小明周末到公園走到十字路口處,記不清前面哪條路通往公園,那么他能一次選對路的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | 0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
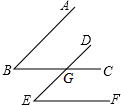 已知:①如圖,AB∥DE,BC∥EF,BC與DE相交于點G.請你猜想∠B與∠E之間具有什么數量關系,并說明理由.②請猜測:如果一個角的兩條邊與另一個角的兩條邊分別平行,那么這兩個角的數量關系是相等或互補.
已知:①如圖,AB∥DE,BC∥EF,BC與DE相交于點G.請你猜想∠B與∠E之間具有什么數量關系,并說明理由.②請猜測:如果一個角的兩條邊與另一個角的兩條邊分別平行,那么這兩個角的數量關系是相等或互補.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com