Question

19．2016年10月17日7時30分，神舟十一號飛船從酒泉衛星發射中心發射升空，隨后與天宮二號首次對接形成組合體，2名航天員景海鵬、陳冬進駐天宮二號，完成了一系列空間科學實驗和技術試驗.33天后，神舟十一號載人飛船返回艙在內蒙古主著陸場成功著陸，天宮二號與神舟十一號載人飛行任務取得圓滿成功，這標志著我國進入航天強國之列．在返回艙返回地面的某一時刻，返回艙P與地面上的兩個測控站A、B恰好處于與地面垂直的同一平面內，此時，在A處測得返回艙P的仰角為60°，在B處測得返回艙P的仰角為45°，已知測控站A、B之間的距離為200千米，求此時返回艙的高度．（結果精確到0.1千米，參考數據：$\sqrt{3}$≈1.732，$\sqrt{2}$≈1.414）

Answer 1

分析 根據題意畫出圖形，設AQ=x，由PQ=AQtan∠PAQ=$\sqrt{3}$x得tan∠PBQ=$\frac{PQ}{BQ}$，即$\frac{\sqrt{3}x}{200+x}=1$，解之得出x的值，從而求得PQ的長．

解答 解：如圖所示，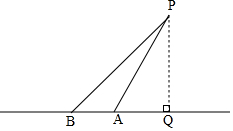

由題意知，∠PAQ=60°，∠PBQ=45°，AB=200，
過點P作PQ⊥BA于點Q，
設AQ=x，
∵在Rt△PAQ中，PQ=AQtan∠PAQ=$\sqrt{3}$x，
∴在Rt△PBQ中，tan∠PBQ=$\frac{PQ}{BQ}$，即$\frac{\sqrt{3}x}{200+x}=1$，
解得：x=100+100$\sqrt{3}$，
則PQ=$\sqrt{3}$x=（100+100$\sqrt{3}$）×$\sqrt{3}$=300+100$\sqrt{3}$≈473.2，
答：此時返回艙的高度約為473.2千米．

點評 本題主要考查解直角三角形的應用-仰角俯角問題，根據題意畫出圖形是解題的根本，熟練掌握三角函數的定義是解題的關鍵．