
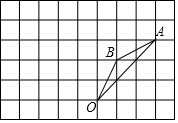
 如圖,在邊長為1的正方形組成的網格中,△AOB的頂點均在格點上,點A,B的坐標分別是A(3,3)、B(1,2),△AOB繞點O逆時針旋轉90°后得到△A1OB1.
如圖,在邊長為1的正方形組成的網格中,△AOB的頂點均在格點上,點A,B的坐標分別是A(3,3)、B(1,2),△AOB繞點O逆時針旋轉90°后得到△A1OB1.分析 (1)根據網格結構找出點A、B繞點O逆時針旋轉90°后的對應點A1、B1的位置,然后順次連接即可,再根據平面直角坐標系寫出各點的坐標;
(2)根據AB掃過的面積等于以OA、OB為半徑的兩個扇形的面積的差列式計算即可得解.
解答 解:(1)如圖,△A1OB1即為所求三角形,A1(-3,3),B1(-2,1);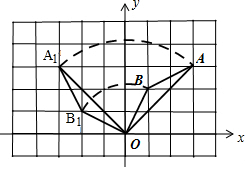
(2)∵OB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,OA=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
∴S扇形OAA1=$\frac{90•π•(3\sqrt{2})^{2}}{360}$=$\frac{9}{2}$π,
S扇形OBB1=$\frac{90•π•(\sqrt{5})^{2}}{360}$=$\frac{5}{4}$π,
則線段AB所掃過的面積為:$\frac{9}{2}$π-$\frac{5}{4}$π=$\frac{13}{4}$π.
點評 本題考查利用旋轉變換作圖,扇形的面積,熟練掌握網格結構,準確找出對應點的位置是解題的關鍵,判斷出AB掃過的面積等于兩個扇形的面積的差是解題的關鍵.


科目:初中數學 來源: 題型:填空題
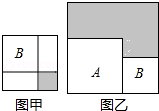 有兩個正方形A,B,現將B放在A的內部得圖甲,將A,B并列放置后構造新的正方形得圖乙.若圖甲和圖乙中陰影部分的面積分別為2和13,則正方形A,B的面積之和為15.
有兩個正方形A,B,現將B放在A的內部得圖甲,將A,B并列放置后構造新的正方形得圖乙.若圖甲和圖乙中陰影部分的面積分別為2和13,則正方形A,B的面積之和為15.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
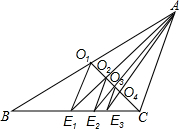 如圖,已知CO1是△ABC的中線,過點O1作O1E1∥AC交BC于點E1,連接AE1交CO1于點O2;過點O2作O2E2∥AC交BC于點E2,連接AE2交CO1于點O3;過點O3作O3E3∥AC交BC于點E3,…,如此繼續,可以依次得到點O4,O5,…,On和點E4,E5,…,En,則O2016E2016=$\frac{1}{2017}$AC.
如圖,已知CO1是△ABC的中線,過點O1作O1E1∥AC交BC于點E1,連接AE1交CO1于點O2;過點O2作O2E2∥AC交BC于點E2,連接AE2交CO1于點O3;過點O3作O3E3∥AC交BC于點E3,…,如此繼續,可以依次得到點O4,O5,…,On和點E4,E5,…,En,則O2016E2016=$\frac{1}{2017}$AC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1600名學生 | |
| B. | 100名學生 | |
| C. | 所抽取的100名學生對“紅軍長征歷史”的知曉情況 | |
| D. | 每一名學生對“紅軍長征歷史”的知曉情況 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,AB為⊙O的直徑,E為⊙O上一點,∠EAB的平分線AC交⊙O于C點,過C點作CD⊥AE交AE的延長線于D點,直線CD與射線AB交于P點.
如圖,AB為⊙O的直徑,E為⊙O上一點,∠EAB的平分線AC交⊙O于C點,過C點作CD⊥AE交AE的延長線于D點,直線CD與射線AB交于P點.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
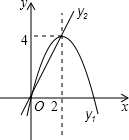 如圖,已知拋物線y1=-x2+4x和直線y2=2x.我們約定:當x任取一值時,x對應的函數值分別為y1、y2,若y1=y2,記M=y1=y2,下列判斷:①當x>2時,M=y2;②當x<0時,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,則x=1.其中正確的有( )
如圖,已知拋物線y1=-x2+4x和直線y2=2x.我們約定:當x任取一值時,x對應的函數值分別為y1、y2,若y1=y2,記M=y1=y2,下列判斷:①當x>2時,M=y2;②當x<0時,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,則x=1.其中正確的有( )| A. | ③④ | B. | ②③ | C. | ②④ | D. | ①④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com