
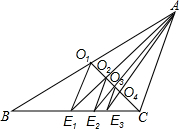
 如圖,已知CO1是△ABC的中線,過點O1作O1E1∥AC交BC于點E1,連接AE1交CO1于點O2;過點O2作O2E2∥AC交BC于點E2,連接AE2交CO1于點O3;過點O3作O3E3∥AC交BC于點E3,…,如此繼續(xù),可以依次得到點O4,O5,…,On和點E4,E5,…,En,則O2016E2016=$\frac{1}{2017}$AC.
如圖,已知CO1是△ABC的中線,過點O1作O1E1∥AC交BC于點E1,連接AE1交CO1于點O2;過點O2作O2E2∥AC交BC于點E2,連接AE2交CO1于點O3;過點O3作O3E3∥AC交BC于點E3,…,如此繼續(xù),可以依次得到點O4,O5,…,On和點E4,E5,…,En,則O2016E2016=$\frac{1}{2017}$AC. 分析 由O1E1∥AC可得出△BO1E1∽△BAC和△E1O1O2∽△ACO2,由相似三角形的性質(zhì)可得出$\frac{B{O}_{1}}{BA}$=$\frac{{O}_{1}{E}_{1}}{AC}$和$\frac{{E}_{1}{O}_{1}}{AC}$=$\frac{{E}_{1}{O}_{2}}{A{O}_{2}}$,結合三角形中位線定理即可得出O2E2=$\frac{1}{3}$AC,同理即可得出OnEn=$\frac{1}{n+1}$AC,再代入n=2016即可得出結論.
解答 解:∵O1E1∥AC,
∴∠BO1E1=∠BAC,∠BE1O1=∠BCA,
∴△BO1E1∽△BAC,
∴$\frac{B{O}_{1}}{BA}$=$\frac{{O}_{1}{E}_{1}}{AC}$.
∵CO1是△ABC的中線,
∴$\frac{B{O}_{1}}{BA}$=$\frac{{O}_{1}{E}_{1}}{AC}$=$\frac{1}{2}$.
∵O1E1∥AC,
∴∠O1E1O2=∠CAO2,∠E1O1O2=∠ACO2,
∴△E1O1O2∽△ACO2,
∴$\frac{{E}_{1}{O}_{1}}{AC}$=$\frac{{E}_{1}{O}_{2}}{A{O}_{2}}$=$\frac{1}{2}$.
∵O2E2∥AC,
∴$\frac{{E}_{1}{O}_{2}}{{E}_{1}A}$=$\frac{{O}_{2}{E}_{2}}{AC}$=$\frac{1}{3}$,
∴O2E2=$\frac{1}{3}$AC.
同理:OnEn=$\frac{1}{n+1}$AC.
∴O2016E2016=$\frac{1}{2016+1}$=$\frac{1}{2017}$.
故答案為:$\frac{1}{2017}$.
點評 本題考查了相似三角形的判定與性質(zhì)以及三角形中位線定理,根據(jù)相似三角形的性質(zhì)找出OnEn=$\frac{1}{n+1}$AC是解題的關鍵.


 提分百分百檢測卷單元期末測試卷系列答案
提分百分百檢測卷單元期末測試卷系列答案科目:初中數(shù)學 來源: 題型:填空題
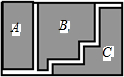 如圖,為方便行人,需在長方形的草坪中修建寬都為1m的小路,將草坪劃分為A,B,C三個區(qū)域,已知原長方形的長為77m,寬為41m,其余部分種植草坪,則草坪的面積為3000平方米.
如圖,為方便行人,需在長方形的草坪中修建寬都為1m的小路,將草坪劃分為A,B,C三個區(qū)域,已知原長方形的長為77m,寬為41m,其余部分種植草坪,則草坪的面積為3000平方米.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 3級 | B. | 4級 | C. | 5級 | D. | 6級 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
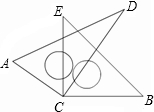 如圖,將帶有45°和30°兩塊直角三角尺的直角頂點C疊放在一起,
如圖,將帶有45°和30°兩塊直角三角尺的直角頂點C疊放在一起,查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
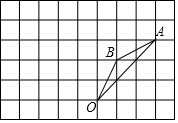 如圖,在邊長為1的正方形組成的網(wǎng)格中,△AOB的頂點均在格點上,點A,B的坐標分別是A(3,3)、B(1,2),△AOB繞點O逆時針旋轉90°后得到△A1OB1.
如圖,在邊長為1的正方形組成的網(wǎng)格中,△AOB的頂點均在格點上,點A,B的坐標分別是A(3,3)、B(1,2),△AOB繞點O逆時針旋轉90°后得到△A1OB1.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com