
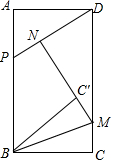
 如圖,在矩形ABCD中,AB=$\sqrt{3}$AD,點P在線段AB上,滿足PB=PD,點M在射線CD上,點C關于直線BM的對稱點為點C′,連接C′B、C′M,射線MC′與射線DP交于點N.
如圖,在矩形ABCD中,AB=$\sqrt{3}$AD,點P在線段AB上,滿足PB=PD,點M在射線CD上,點C關于直線BM的對稱點為點C′,連接C′B、C′M,射線MC′與射線DP交于點N.分析 (1)先設出AP,表示出BP,PD,進而用勾股定理求出x=$\frac{\sqrt{3}}{3}$AD,再用三角函數求出∠ADP=30°,即可得出結論;
(2)先求出∠CBH=120°,再判斷出Rt△BHN≌Rt△BC'N,得出∠HBN=∠C'BN,進行代換即可得出結論;
(3)同(2)的方法判斷出HN=NC',再求出PH,即可得出結論.
解答 解:(1)設AP=x,
∴PB=AB-AP=AB-x,
∵AB=$\sqrt{3}$AD,
∴BP=$\sqrt{3}$AD-x,
∵PB=PD,
∴PD=$\sqrt{3}$AD-x,
∴四邊形ABCD是矩形,
∴BC=AD,∠C=∠A=∠ABC∠ADC=90°,
在Rt△ADP中,AP=x,PD=$\sqrt{3}$AD-x,
根據勾股定理得,AD2+AP2=PD2,
∴AD2+x2=($\sqrt{3}$AD-x)2,
∴x=$\frac{\sqrt{3}}{3}$AD,
∴tan∠ADP=$\frac{AP}{AD}$=$\frac{\sqrt{3}}{3}$,
∴∠ADP=30°,
∴∠PDC=90°-∠ADP=60°;
(2)如圖1,
過點B作BH⊥DP交DP的延長線于H,
由(1)知,BP=$\sqrt{3}$AD-x=$\frac{2\sqrt{3}}{3}$AD,∠ADP=30°,
∴∠BPH=∠APD=60°,BH=AD=BC,
∴∠PBH=30°,
∴∠CBH=120°,
∵點C關于直線BM的對稱點為點C′,
∴BC'=BC=AD,∠CBM=∠C'BM,∠BC'M=∠C=90°,
∴∠BC'N=90°,
在Rt△BHN和Rt△BC'N中,$\left\{\begin{array}{l}{BH=BC'}\\{BN=BN}\end{array}\right.$,
∴Rt△BHN≌Rt△BC'N,
∴∠HBN=∠C'BN,
∴∠CBH=∠HBN+∠C'BN+∠C'BM+∠CBM=120°,
∴∠MBN=∠C'BN+∠C'BM=$\frac{1}{2}$(∠HBN+∠C'BN+∠C'BM+∠CBM)=60°,
即:當M在線段CD上時,∠MBN=60°;
(3)如圖3,∵AB=$\sqrt{3}$AD=9,
∴AD=3$\sqrt{3}$, 過點B作BH⊥DP交DP的延長線于H,
過點B作BH⊥DP交DP的延長線于H,
由(1)知,BP=$\sqrt{3}$AD-x=$\frac{2\sqrt{3}}{3}$AD=6,∠ADP=30°,
∴∠BPH=∠APD=60°,BH=AD=BC,
∴∠PBH=30°,
∴∠CBH=120°,
∵點C關于直線BM的對稱點為點C′,
∴BC'=BC=AD,∠CBM=∠C'BM,∠BC'M=∠C=90°,
∴∠BC'N=90°,
在Rt△BHN和Rt△BC'N中,$\left\{\begin{array}{l}{BH=BC'}\\{BN=BN}\end{array}\right.$,
∴Rt△BHN≌Rt△BC'N,
∴HN=NC',在Rt△BPH中,∠BPH=60°,BP=6,
∴PH=3,
∴NP=PH+HN=3+NH=3+NC',
∴NP-NC'=3.
故答案為:NP-NC'=3.
點評 此題是四邊形綜合題,主要考查了對稱的性質,全等三角形的判定和性質,勾股定理,含30°的直角三角形的性質,解本題的關鍵是判斷出Rt△BHN≌Rt△BC'N,難點是(3)作出圖形,是一道很好的中考常考題.


科目:初中數學 來源: 題型:解答題
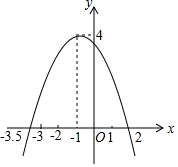 如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點(2,0)和(-3.5,0),頂點為(-1,4),根據圖象直接寫出下列答案.
如圖,二次函數y=ax2+bx+c(a≠0)的圖象與x軸交于點(2,0)和(-3.5,0),頂點為(-1,4),根據圖象直接寫出下列答案.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①abc<0;②b2-4ac>0;③m>2;④當x<0時,y隨x的增大而增大.其中正確結論的個數是( )
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,且關于x的一元二次方程ax2+bx+c-m=0沒有實數根,有下列結論:①abc<0;②b2-4ac>0;③m>2;④當x<0時,y隨x的增大而增大.其中正確結論的個數是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 有理數a、b、c在數軸上的位置如圖所示,化簡|a-b|+|c-a|-|b-c|的結果是( )
有理數a、b、c在數軸上的位置如圖所示,化簡|a-b|+|c-a|-|b-c|的結果是( )| A. | -2a | B. | -2b | C. | -2a-2b | D. | 2a-2b |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 已知二次函數y=ax2+bx+c的圖象如圖所示,則下列結論正確的個數為( )
已知二次函數y=ax2+bx+c的圖象如圖所示,則下列結論正確的個數為( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com