Question

5．提出問題：當x＞0時如何求函數y=x+$\frac{1}{x}$的最大值或最小值？
分析問題：前面我們剛剛學過二次函數的相關知識，知道求二次函數的最值時，我們可以利用它的圖象進行猜想最值，或利用配方可以求出它的最值．
例如我們求函數y=x-2$\sqrt{x}$（x＞0）的最值時，就可以仿照二次函數利用配方求最值的方法解決問題；y=x-2$\sqrt{x}$=（$\sqrt{x}$）²-2$\sqrt{x}$-2$\sqrt{x}$+1-1=（$\sqrt{x}$-1）²-1即當x=1時，y有最小值為-1
解決問題
借鑒我們已有的研究函數的經驗，探索函數y=x+$\frac{1}{x}$（x＞0）的最大（小）值．
（1）實踐操作：填寫下表，并用描點法畫出函數y=x+$\frac{1}{x}$（x＞0）的圖象：

x	…	$\frac{1}{4}$	$\frac{1}{3}$	$\frac{1}{2}$	1	2	3	4	…
y	…								…

（2）觀察猜想：觀察該函數的圖象，猜想
當x=1時，函數y=x+$\frac{1}{x}$（x＞0）有最小值（填“大”或“小”），是2．
（3）推理論證：利用上述例題，請你嘗試通過配方法求函數y=x+$\frac{1}{x}$（x＞0）的最大（小）值，以證明你的猜想．知識能力運用：直接寫出函數y=-2x-$\frac{1}{2x}$（x＞0）當x=$\frac{1}{2}$時，該函數有最大值（填“大”或“小”），是-2．

Answer 1

分析 （1）由x的值計算出y的值，填表即可；用描點法畫出圖象即可；
（2）用配方法得出y=x+$\frac{1}{x}$=（$\sqrt{x}$-$\frac{1}{\sqrt{x}}$）²+2，即可得出結果；
（3）用配方法得出y=-2x-$\frac{1}{2x}$=-（$\sqrt{2x}$-$\frac{1}{\sqrt{2x}}$）²-2，即可得出結果．

解答 解：（1）當x=$\frac{1}{4}$時，y=x+$\frac{1}{x}$=$\frac{1}{4}$+4=4$\frac{1}{4}$；
當x=$\frac{1}{3}$時，y=x+$\frac{1}{x}$=$\frac{1}{3}$+3=3$\frac{1}{3}$；
當x=$\frac{1}{2}$時，y=x+$\frac{1}{x}$=$\frac{1}{2}$+2=2$\frac{1}{2}$；
當x=1時，y=x+$\frac{1}{x}$=1+1=2；
當x=2時，y=x+$\frac{1}{x}$=2+$\frac{1}{2}$=2$\frac{1}{2}$；
當x=3時，y=x+$\frac{1}{x}$=3+$\frac{1}{3}$=3$\frac{1}{3}$；
當x=4時，y=x+$\frac{1}{x}$=4+$\frac{1}{4}$=4$\frac{1}{4}$；填表如下：
函數圖象如圖所示：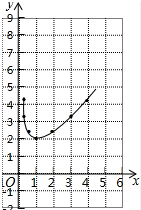
（2）∵y=x+$\frac{1}{x}$=（$\sqrt{x}$）²+（$\frac{1}{\sqrt{x}}$）²=（$\sqrt{x}$-$\frac{1}{\sqrt{x}}$）²+2，
∴當x=1時，函數y=x+$\frac{1}{x}$（x＞0）有最小值，最小值為2；
故答案為：1，小，2；
（3）∵y=-2x-$\frac{1}{2x}$=-（2x+$\frac{1}{2x}$）=-（$\sqrt{2x}$-$\frac{1}{\sqrt{2x}}$）²-2，
∴當$\sqrt{2x}$=1，即x=$\frac{1}{2}$時，函數y=-2x-$\frac{1}{2x}$（x＞0）有最大值，最大值為-2；
故答案為：$\frac{1}{2}$，大，-2．

點評 本題是函數綜合題目，考查了用描點法畫函數的圖象、函數的最值問題、配方法的應用；本題綜合性強，難度較大，用配方法求出函數的最值是解決問題的關鍵．