
 在如圖所示的正方形網格中,每個小正方形的邊長皆為1.請在網格上畫出長度分別為$\sqrt{2}$,$\sqrt{5}$,$\sqrt{17}$的線段.
在如圖所示的正方形網格中,每個小正方形的邊長皆為1.請在網格上畫出長度分別為$\sqrt{2}$,$\sqrt{5}$,$\sqrt{17}$的線段. 分析 由勾股定理得出:$\sqrt{2}$是直角邊長為1,1的直角三角形的斜邊;$\sqrt{5}$是直角邊長為1,2的直角三角形的斜邊;$\sqrt{17}$是直角邊長為1,4的直角三角形的斜邊.
解答  解:如圖所示,圖中的AB,CD,EF即為所求,
解:如圖所示,圖中的AB,CD,EF即為所求,
AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,CD=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,EF=$\sqrt{{4}^{2}+{1}^{2}}$=$\sqrt{17}$.
點評 本題考查了勾股定理;解決本題的關鍵是找到無理數是直角邊長為哪兩個有理數的直角三角形的斜邊長.


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案科目:初中數學 來源: 題型:選擇題
| A. | y=2(x+4)2+5 | B. | y=2(x-4)2+5 | C. | y=2(x+4)2-5 | D. | y=2(x-4)2-5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
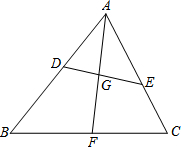 如圖,在△ABC中,D,E分別是AB,AC上的點,∠AED=∠ABC,∠BAC的平分線AF交DE于點G,交BC于點F.
如圖,在△ABC中,D,E分別是AB,AC上的點,∠AED=∠ABC,∠BAC的平分線AF交DE于點G,交BC于點F.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,數軸上點A,B表示的數分別為-40,50.現有一動點P以2個單位每秒的速度從點A向B運動,另一動點Q以3個單位每秒的速度從點B向A運動.當AQ=3PQ時,運動的時間為( )
如圖,數軸上點A,B表示的數分別為-40,50.現有一動點P以2個單位每秒的速度從點A向B運動,另一動點Q以3個單位每秒的速度從點B向A運動.當AQ=3PQ時,運動的時間為( )| A. | 15秒 | B. | 20秒 | C. | 15秒或25秒 | D. | 15秒或20秒 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | ∠α的補角和∠β的補角相等 | B. | ∠α的余角和∠β的補角相等 | ||
| C. | ∠α的余角和∠β的補角互余 | D. | ∠α的余角和∠β的補角互補 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
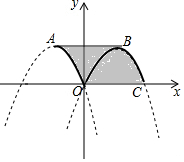 已知函數y=$\left\{\begin{array}{l}{-(x+1)^{2}+1(-1≤x<0)}\\{-(x-1)^{2}+1(0≤x≤2)}\end{array}\right.$,其圖象如圖中的實線部分,圖象上兩個最高點分別是A,B,連接AB,則圖中曲四邊形ABCO(陰影部分)的面積是2.
已知函數y=$\left\{\begin{array}{l}{-(x+1)^{2}+1(-1≤x<0)}\\{-(x-1)^{2}+1(0≤x≤2)}\end{array}\right.$,其圖象如圖中的實線部分,圖象上兩個最高點分別是A,B,連接AB,則圖中曲四邊形ABCO(陰影部分)的面積是2.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
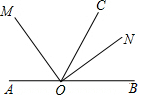 如圖,點O是直線AB上一點,OM平分∠AOC,ON平分∠BOC.
如圖,點O是直線AB上一點,OM平分∠AOC,ON平分∠BOC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com