Question

15．如圖①，△ABC是正三角形，△BDC是頂角∠BDC=120°的等腰三角形，以D為頂點作一個60°角，角兩邊分別交AB，AC邊于M，N兩點，連接MN．
（I）探究：線段BM，MN，NC之間的關系，并加以證明．
提示：看到這個問題后，小明猜想：BM+NC=MN，并且通過延長AC到點E，使得CE=BM，連接DE，再證明三角形全等，請你按照小明的思路寫出證明過程．
（Ⅱ）若點M是AB的延長線上的一點，N是CA的延長線上的點，其它條件不變，請你再探線段BM，MN，NC之間的關系，在圖②中畫出圖形，并說明理由．

Answer 1

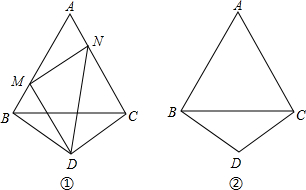
分析 （1）延長AC至E，使得CE=BM并連接DE，構造全等三角形，找到相等的線段，MD=DE，再進一步證明△DMN≌△DEN，進而得到MN=BM+NC．
（2）按要求作出圖形，先證△BMD≌△CED，再證△MDN≌△EDN（SAS），即可得出結論．

解答 解：（1）MN=BM+NC．理由如下：
延長AC至E，使得CE=BM（或延長AB至E，使得BE=CN），并連接DE．
∵△BDC為等腰三角形，△ABC為等邊三角形，
∴BD=CD，∠DBC=∠DCB，∠MBC=∠ACB=60°，
又BD=DC，且∠BDC=120°，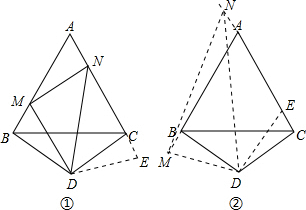
∴∠DBC=∠DCB=30°
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°，
∴∠MBD=∠ECD=90°，
在△MBD與△ECD中，
∵$\left\{\begin{array}{l}{BD=CD}\\{∠MBD=∠ECD}\\{EC=BM}\end{array}\right.$，
∴△MBD≌△ECD（SAS），
∴MD=DE，
∴△DMN≌△DEN，
∴MN=BM+NC．

（2）如圖②中，結論：MN=NC-BM．
理由：在CA上截取CE=BM．
∵△ABC是正三角形，
∴∠ACB=∠ABC=60°，
又∵BD=CD，∠BDC=120°，
∴∠BCD=∠CBD=30°，
∴∠MBD=∠DCE=90°，
在△BMD和△CED中
∵$\left\{\begin{array}{l}{EC=BM}\\{∠MBD=∠DCE}\\{BD=DC}\end{array}\right.$，
∴△BMD≌△CED（SAS），
∴DE=DM，
在△MDN和△EDN中
∵$\left\{\begin{array}{l}{ND=ND}\\{∠EDN=∠MDN}\\{MD=ED}\end{array}\right.$，
∴△MDN≌△EDN（SAS），
∴MN=NE=NC-CE=NC-BM．

點評 此題考查了全等三角形的判定與性質、等邊三角形的性質、等腰三角形的性質等知識，解題的關鍵是學會添加常用輔助線，構造全等三角形解決問題，屬于中考常考題型．