
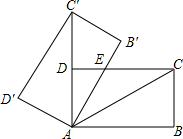
 如圖,將矩形ABCD繞點(diǎn)A旋轉(zhuǎn)至矩形AB'C'D'位置,此時(shí)AC'的中點(diǎn)恰好與D點(diǎn)重合,AB'交CD于點(diǎn)E,若AD=3,則△AEC的面積為( )
如圖,將矩形ABCD繞點(diǎn)A旋轉(zhuǎn)至矩形AB'C'D'位置,此時(shí)AC'的中點(diǎn)恰好與D點(diǎn)重合,AB'交CD于點(diǎn)E,若AD=3,則△AEC的面積為( )| A. | 12 | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 6 |
分析 根據(jù)旋轉(zhuǎn)后AC的中點(diǎn)恰好與D點(diǎn)重合,利用旋轉(zhuǎn)的性質(zhì)得到直角三角形ACD中,∠ACD=30°,再由旋轉(zhuǎn)后矩形與已知矩形全等及矩形的性質(zhì)得到∠DAE為30°,進(jìn)而得到∠EAC=∠ECA,利用等角對(duì)等邊得到AE=CE,根據(jù)正切的概念求出CD,確定出EC的長,即可求出三角形AEC面積.
解答 解:由旋轉(zhuǎn)的性質(zhì)可知:AC=AC',
∵D為AC'的中點(diǎn),
∴AD=$\frac{1}{2}$AC,
∵ABCD是矩形,
∴AD⊥CD,
∴∠ACD=30°,
∵AB∥CD,
∴∠CAB=30°,
∴∠C'AB'=∠CAB=30°,
∴∠EAC=30°,
∴AE=EC,
∴DE=$\frac{1}{2}$AE=$\frac{1}{2}$CE,
∴CE=2DE,
CD=$\sqrt{3}$AD=3$\sqrt{3}$,
∴EC=2$\sqrt{3}$,
∴△AEC的面積=$\frac{1}{2}$×EC×AD=3$\sqrt{3}$,
故選:C.
點(diǎn)評(píng) 本題考查了旋轉(zhuǎn)的性質(zhì)、矩形的性質(zhì)、特殊角的三角函數(shù),三角形面積計(jì)算等知識(shí)點(diǎn),清楚旋轉(zhuǎn)的“不變”特性是解答的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
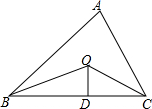 如圖,已知△ABC的周長是21,OB,OC分別平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面積是( )
如圖,已知△ABC的周長是21,OB,OC分別平分∠ABC和∠ACB,OD⊥BC于,且OD=4,△ABC的面積是( )| A. | 25 | B. | 84 | C. | 42 | D. | 21 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| 人員 | 經(jīng)理 | 廚師 | 會(huì)計(jì) | 保安 | 服務(wù)員 |
| 人數(shù)(人) | 1 | 2 | 1 | 1 | 5 |
| 工資(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | a-3<b-3 | B. | 3-a<3-b | C. | $\frac{1}{3}$a<$\frac{1}{3}$b | D. | -2a>-2b |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | y2-4y+5=0 | B. | y2-4y-5=0 | C. | y2+4y-5=0 | D. | y2+4y+5=0 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com