
 已知:如圖,O為坐標原點,四邊形OABC為長方形,A(10,0),C(0,4),點D是OA的中點,點P在BC上運動.
已知:如圖,O為坐標原點,四邊形OABC為長方形,A(10,0),C(0,4),點D是OA的中點,點P在BC上運動.分析 (1)當P1O=OD=5或P2O=P2D或P3D=OD=5或P4D=OD=5時分別作P2E⊥OA于E,DF⊥BC于F,P4G⊥OA于G,利用勾股定理P1C,OE,P3F,DG的值,就可以求出P的坐標;
(2)作點D關于BC的對稱點D′,連接OD′交BC于P,則這時的△POD的周長最小,即△POD的周長=OD′+OD,根據(jù)勾股定理得到OD′=$\sqrt{O{D}^{2}+DD{′}^{2}}$=$\sqrt{91}$,于是得到結論.
解答 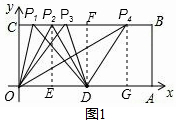 解:(1)當P1O=OD=5時,由勾股定理可以求得P1C=3,
解:(1)當P1O=OD=5時,由勾股定理可以求得P1C=3,
P2O=P2D時,作P2E⊥OA,
∴OE=ED=2.5;
當P3D=OD=5時,作DF⊥BC,由勾股定理,得P3F=3,
∴P3C=2;
當P4D=OD=5時,作P4G⊥OA,由勾股定理,得
DG=3,
∴OG=8.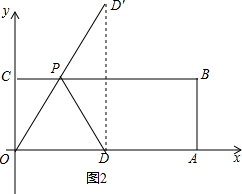
∴P1(2,4),P2(2.5,4),P3(3,4),P4(8,4);
(2)作點D關于BC的對稱點D′,連接OD′交BC于P,
則這時的△POD的周長最小,
△POD的周長=OD′+OD,
∵點D是OA的中點,
∴OD=5,DD′=8,
∴OD′=$\sqrt{O{D}^{2}+DD{′}^{2}}$=$\sqrt{89}$,
∴△POD的周長=$\sqrt{89}$+5.
點評 本題考查了軸對稱-最小距離問題,矩形的性質,坐標與圖形的性質,等腰三角形的性質,平行四邊形的判定及性質,菱形的判定及性質,勾股定理的運用.


 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
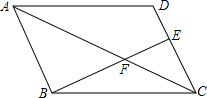 如圖,在平行四邊形ABCD中,E在DC邊上,若DE:EC=1:2,則△CEF與△ABF的面積比為( )
如圖,在平行四邊形ABCD中,E在DC邊上,若DE:EC=1:2,則△CEF與△ABF的面積比為( )| A. | 1:4 | B. | 2:3 | C. | 4:9 | D. | 1:9 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,在平面直角坐標系中,A(1,2),B(3,1),C(-2,-1).
如圖,在平面直角坐標系中,A(1,2),B(3,1),C(-2,-1).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com