
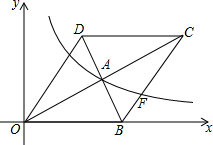
 如圖,在平面直角坐標系中,菱形OBCD的邊OB在x軸上,反比例函數y=$\frac{k}{x}$(x>0)的圖象經過菱形對角線的交點A,且與邊BC交于點F,點A的坐標為(4,2).則點F的坐標是(6,$\frac{4}{3}$).
如圖,在平面直角坐標系中,菱形OBCD的邊OB在x軸上,反比例函數y=$\frac{k}{x}$(x>0)的圖象經過菱形對角線的交點A,且與邊BC交于點F,點A的坐標為(4,2).則點F的坐標是(6,$\frac{4}{3}$). 分析 將點A的坐標代入到反比例函數的一般形式后求得k值即可確定函數的解析式,過點A作AM⊥x軸于點M,過點C作CN⊥x軸于點N,首先求得點B的坐標,然后求得直線BC的解析式,求得直線和雙曲線的交點坐標即可.
解答 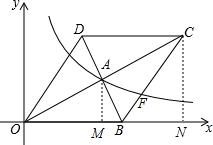 解:∵反比例函數y=$\frac{k}{x}$的圖象經過點A,A點的坐標為(4,2),
解:∵反比例函數y=$\frac{k}{x}$的圖象經過點A,A點的坐標為(4,2),
∴k=2×4=8,
∴反比例函數的解析式為y=$\frac{8}{x}$;
過點A作AM⊥x軸于點M,過點C作CN⊥x軸于點N,
由題意可知,CN=2AM=4,ON=2OM=8,
∴點C的坐標為C(8,4),
設OB=x,則BC=x,BN=8-x,
在Rt△CNB中,x2-(8-x)2=42,
解得:x=5,
∴點B的坐標為B(5,0),
設直線BC的函數表達式為y=ax+b,
∵直線BC過點B(5,0),C(8,4),
∴$\left\{\begin{array}{l}{5a+b=0}\\{8a+b=4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{4}{3}}\\{b=-\frac{20}{3}}\end{array}\right.$,
∴直線BC的解析式為y=$\frac{4}{3}$x-$\frac{20}{3}$,
根據題意得方程組$\left\{\begin{array}{l}{y=\frac{4}{3}x-\frac{20}{3}}\\{y=\frac{8}{x}}\end{array}\right.$,
解此方程組得:$\left\{\begin{array}{l}{x=-1}\\{y=-8}\end{array}\right.$或$\left\{\begin{array}{l}{x=6}\\{y=\frac{4}{3}}\end{array}\right.$.
∵點F在第一象限,
∴點F的坐標為(6,$\frac{4}{3}$).
故答案為:(6,$\frac{4}{3}$).
點評 本題考查了反比例函數圖象上的點的坐標特點、待定系數法確定反比例函數的解析式等知識,解題的關鍵是能夠根據點C的坐標確定點B的坐標,從而確定直線的解析式.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
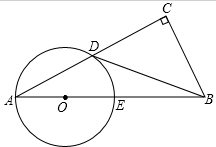 如圖,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,過點A,D作⊙O,使圓心O在AB上,⊙O與AB交于點E.
如圖,在Rt△ABC中,∠C=90°,且∠A+∠CDB=90°,過點A,D作⊙O,使圓心O在AB上,⊙O與AB交于點E.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 有一個角是直角的四邊形是菱形 | |
| B. | 對角線互相垂直的菱形是正方形 | |
| C. | 對角線相等的平行四邊形是矩形 | |
| D. | 一組鄰邊相等的平行四邊形是正方形 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
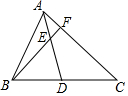 如圖,AD是△ABC的中線,E是AD上一點,且AE:ED=1:2,BE的延長線交AC于F,則AF:FC=( )
如圖,AD是△ABC的中線,E是AD上一點,且AE:ED=1:2,BE的延長線交AC于F,則AF:FC=( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com