Question

10．如圖?，在正方形ABCD中，E是AB上一點，F是AD延長線上一點，且DF=BE．

（1）求證：CE=CF；
（2）在圖1中，若G在AD上，且∠GCE=45°，證明：GE=BE+GD；
（3）根據你所學的知識，運用（1）、（2）解答中積累的經驗，完成下題：
如圖2，在直角梯形ABCD中，AD∥BC（BC＞AD），∠B=90°，E是AB的中點，且∠DCE=45°，求AD的長．

Answer 1

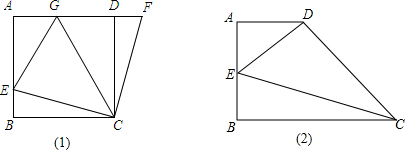
分析 （1）根據正方形的性質可得BC=DC，∠B=∠FDC=90°，再證明△CBE≌△CDF可得CE=CF；
（2）首先證明∠GCF=∠GCE，然后證明△ECG≌△FCG，根據全等三角形的性質可得GE=GF=DG+DF=DG+BE．
（3）過點C作CG⊥AD交AD的延長線于點G，利用勾股定理求得DE的長．

解答 解：（1）證明：∵四邊形ABCD是正方形，
∴BC=DC，∠B=∠FDC=90°，
在△EBC和△FDC中，
$\left\{\begin{array}{l}{DF=EB}\\{∠FDC=∠B}\\{CB=DC}\end{array}\right.$，
∴△CBE≌△CDF（SAS），
∴CE=CF；
（2）由（1）得：△CBE≌△CDF，
∴∠BCE=∠DCF，
∴∠BCE+∠ECD=∠DCF+∠ECD，
即∠ECF=∠BCD=90°，
又∵∠GCE=45°，
∴∠GCF=∠GCE=45°，
∵在△ECG≌△FCG中，
$\left\{\begin{array}{l}{CE=CF}\\{∠GCE=∠GCF}\\{GC=GC}\end{array}\right.$，
∴△ECG≌△FCG（SAS），
∴GE=GF=DG+DF=DG+BE；
（3）如圖2，過點C作CG⊥AD交AD的延長線于點G，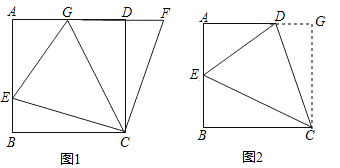
由（2）和題設知：DE=DG+BE，
設DG=x，則AD=AB-x，DE=x+$\frac{1}{2}$AB，
在Rt△ADE中，由勾股定理，得：
AD²+AE²=DE²
∴（AB-x）²+（$\frac{1}{2}$AB）²=（x+$\frac{1}{2}AB$）²
解得x=$\frac{1}{3}AB$．
∴AD=$\frac{2}{3}AB$．

點評 此題主要考查了正方形的性質，關鍵是掌握正方形四邊相等，四個角都是直角．