
 如圖,已知△ABC,△DCE,△FEG是三個全等的等腰三角形,底邊BC,CE,EG在同一直線上,且AB=$\sqrt{3}$,BC=1,連結(jié)BF,分別交AC,DC,DE于點(diǎn)P,Q,R.
如圖,已知△ABC,△DCE,△FEG是三個全等的等腰三角形,底邊BC,CE,EG在同一直線上,且AB=$\sqrt{3}$,BC=1,連結(jié)BF,分別交AC,DC,DE于點(diǎn)P,Q,R.分析 (1)已知三個全等的等腰三角形,以及邊長,所以可求得各線段的長,即可求得線段的比值,由公共角即可證得△BFG∽△FEG;
(2)利用△BPC~△BFG求得PC的長,進(jìn)而可知AP的長,即可得答案.
(3)可以提問求證:∠PCB=∠REC,這個問題只需要運(yùn)用兩直線平行,同位角相等進(jìn)行解答.此題為發(fā)散性題型,不唯一.
解答 解:(1)據(jù)題意知BC=CE=EG=1,BG=3,F(xiàn)G=AB=$\sqrt{3}$,
在△BFG和△FEG中,
∵$\frac{FG}{EG}$=$\frac{BG}{FG}$=$\sqrt{3}$,∠G=∠G
∴△BFG∽△FEG;
(2)∵△ABC≌△FEG,
∴∠ACB=∠G,
∴PC∥FG,
∴△BPC~△BFG,
∴$\frac{PC}{BC}$=$\frac{FG}{BG}$,即 $\frac{PC}{1}$=$\frac{\sqrt{3}}{3}$,
解得:PC=$\frac{\sqrt{3}}{3}$,
∵AC=AB=$\sqrt{3}$,
∴AP=AC-PC=$\frac{2\sqrt{3}}{3}$,
∴$\frac{AP}{PC}$=$\frac{\frac{2\sqrt{3}}{3}}{\frac{\sqrt{3}}{3}}$=2.
(3)①求證:∠PCB=∠REB,②求證:PC∥RE,答案不唯一.
證明:∵△ABC≌△DCE,
∴∠PCB=∠REB,
∴PC∥RE.
點(diǎn)評 本題主要考查了相似三角形的判定與性質(zhì)及全等三角形、等腰三角形的性質(zhì)運(yùn)用,熟練掌握相似三角形的判定與性質(zhì)是解題的關(guān)鍵.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3000x2=7500 | B. | 3000(1+x)2=7500 | ||
| C. | 3000(1+x%)2=7500 | D. | 3000(1+x)+3000(1+x)2=7500 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
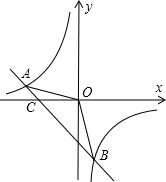 如圖,已知A(-4,n),B(2,-4)是一次函數(shù)y=kx+b的圖象和反比例函數(shù)y=$\frac{m}{x}$的圖象的兩個交點(diǎn).
如圖,已知A(-4,n),B(2,-4)是一次函數(shù)y=kx+b的圖象和反比例函數(shù)y=$\frac{m}{x}$的圖象的兩個交點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 13cm,12cm,20cm | B. | 8cm,7cm,15cm | C. | 5cm,5cm,11cm | D. | 3cm,4cm,8cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
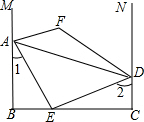 如圖,AB⊥BC,AE平分∠BAD交BC于點(diǎn)E,AE⊥DE,∠1+∠2=90°,M、N分別是BA、CD延長線上的點(diǎn),∠EAM和∠EDN的平分線交于點(diǎn)F.∠F的度數(shù)為( )
如圖,AB⊥BC,AE平分∠BAD交BC于點(diǎn)E,AE⊥DE,∠1+∠2=90°,M、N分別是BA、CD延長線上的點(diǎn),∠EAM和∠EDN的平分線交于點(diǎn)F.∠F的度數(shù)為( )| A. | 120° | B. | 135° | C. | 150° | D. | 不能確定 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com