
分析 問題1:利用題中的不等式得到x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,從而得到x=2時,周長的最小值為8;
問題2:先變形得到$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+16}{x+1}$=x+1+$\frac{16}{x+1}$,然后利用題中的不等式性質解決問題;
問題3:設學校學生人數為x人,生均投入為y元,依題意得y=$\frac{6400+10x+0.01{x}^{2}}{x}$,變形得到y=$\frac{x}{100}$+$\frac{6400}{x}$+10,然后利用不等式的性質求解.
解答 解:問題1:∵x+$\frac{4}{x}$≥2$\sqrt{x•\frac{4}{x}}$=4,當x=$\frac{4}{x}$時,2(x+$\frac{4}{x}$)有最小值8,
即x=2時,周長的最小值為8;
問題2:$\frac{{y}_{2}}{{y}_{1}}$=$\frac{(x+1)^{2}+16}{x+1}$=x+1+$\frac{16}{x+1}$,
∵x+1+$\frac{16}{x+1}$≥2$\sqrt{(x+1)•\frac{16}{x+1}}$=8,即x+1=$\frac{16}{x+1}$時,$\frac{{y}_{2}}{{y}_{1}}$有最小值,即x=3時,$\frac{{y}_{2}}{{y}_{1}}$的最小值為8;
故答案為2,8;3,8;
問題3:設學校學生人數為x人,生均投入為y元,依題意得:
y=$\frac{6400+10x+0.01{x}^{2}}{x}$=$\frac{x}{100}$+$\frac{6400}{x}$+10,
∵x>0,
∴y=$\frac{x}{100}$+$\frac{6400}{x}$+10=$\frac{1}{100}$(x+$\frac{640000}{x}$)+10≥$\frac{2}{100}$$\sqrt{640000}$+10=16+10,
∴當x=$\frac{640000}{x}$,即x=800時,即x=800時,y取最小值26.
答:當學校學生人數為800人時,該校每天生均投入最低,最低費用是26元.
點評 本題考查了二次函數的應用:幾何圖形中的二次函數問題常見的有:幾何圖形中面積的最值,用料的最佳方案以及動態幾何中的最值的討論.也考查了閱讀理解能力.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
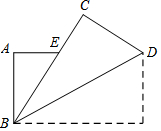 如圖,把長方形紙片ABCD紙沿對角線折疊,設重疊部分為△EBD,那么,有下列說法:
如圖,把長方形紙片ABCD紙沿對角線折疊,設重疊部分為△EBD,那么,有下列說法:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
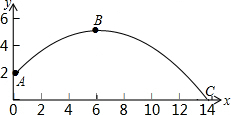 九年級的一名男生在體育課上測試推實心球成績,已知實心球所經過的路線是某二次函數圖象的一部分,如圖所示.若這個男生出手處A點的坐標為(0,2),實心球路線的最高處B點的坐標為B(6,5).
九年級的一名男生在體育課上測試推實心球成績,已知實心球所經過的路線是某二次函數圖象的一部分,如圖所示.若這個男生出手處A點的坐標為(0,2),實心球路線的最高處B點的坐標為B(6,5).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com