
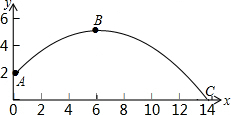
 九年級的一名男生在體育課上測試推實心球成績,已知實心球所經過的路線是某二次函數圖象的一部分,如圖所示.若這個男生出手處A點的坐標為(0,2),實心球路線的最高處B點的坐標為B(6,5).
九年級的一名男生在體育課上測試推實心球成績,已知實心球所經過的路線是某二次函數圖象的一部分,如圖所示.若這個男生出手處A點的坐標為(0,2),實心球路線的最高處B點的坐標為B(6,5).分析 (1)根據拋物線的頂點坐標,設其頂點式,由A坐標可得答案;
(2)令y=0,解方程求得x的值即可.
解答 解:(1)設拋物線解析式為y=a(x-6)2+5(a≠0),
∵A(0,2)在拋物線上,
∴代入得a=-$\frac{1}{12}$,
∴拋物線的解析式為y=-$\frac{1}{12}$(x-6)2+5.
(2)∵令y=0,即-$\frac{1}{12}$(x-6)2+5=0,解得x1=6-2$\sqrt{15}$(舍去),x2=6+2$\sqrt{15}$
∴OC=6+2$\sqrt{15}$.
答:該同學把實心球扔出(6+2$\sqrt{15}$)m.
點評 本題考查的是二次函數的應用,熟知利用待定系數法求二次函數的解析式是解答此題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
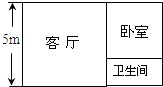 如圖,有一長方形的倉庫,一邊長為5m,現要將它改建為簡易住房,改建后的住房分為客廳、臥室和衛生間三部分,其中客廳和臥室都為正方形,且臥室的面積大于衛生間的面積,若改建后衛生間的面積為6m2,則長方形倉庫另一邊的長是8m.
如圖,有一長方形的倉庫,一邊長為5m,現要將它改建為簡易住房,改建后的住房分為客廳、臥室和衛生間三部分,其中客廳和臥室都為正方形,且臥室的面積大于衛生間的面積,若改建后衛生間的面積為6m2,則長方形倉庫另一邊的長是8m.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com