
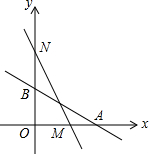
 如圖,直線L:y=-$\frac{1}{2}$x+2與x軸、y軸分別交于A、B兩點,在y軸上有一點N(0,4),動點M從A點以每秒1個單位的速度勻速沿x軸向左移動.
如圖,直線L:y=-$\frac{1}{2}$x+2與x軸、y軸分別交于A、B兩點,在y軸上有一點N(0,4),動點M從A點以每秒1個單位的速度勻速沿x軸向左移動.分析 (1)在y=-$\frac{1}{2}$x+2中,令別令y=0和x=0,則可求得A、B的坐標;
(2)利用t可表示出OM,則可表示出S,注意分M在y軸右側和左側兩種情況;
(3)由全等三角形的性質可得OM=OB=2,則可求得M點的坐標;
(4)由折疊的性質可知MG平分∠OMN,利用角平分線的性質定理可得到$\frac{OG}{NG}$=$\frac{OM}{MN}$,則可求得OG的長,可求得G點坐標.
解答 解:
(1)在y=-$\frac{1}{2}$x+2中,令y=0可求得x=4,令x=0可求得y=2,
∴A(4,0),B(0,2),
故答案為:(4,0);(0,2);
(2)由題題意可知AM=t,
①當點M在y軸右邊時,OM=OA-AM=4-t,
∵N(0,4),
∴ON=4,
∴S=$\frac{1}{2}$OM•ON=$\frac{1}{2}$×4×(4-t)=8-2t;
②當點M在y軸左邊時,則OM=AM-OA=t-4,
∴S=$\frac{1}{2}$×4×(t-4)=2t-8;
(3)∵△NOM≌△AOB,
∴MO=OB=2,
∴M(2,0);
(4)∵OM=2,ON=4,
∴MN=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∵△MGN沿MG折疊,
∴∠NMG=∠OMG,
∴$\frac{OG}{NG}$=$\frac{OM}{MN}$,且NG=ON-OG,
∴$\frac{OG}{4-OG}$=$\frac{2}{2\sqrt{5}}$,解得OG=$\sqrt{5}$-1,
∴G(0,$\sqrt{5}$-1).
點評 本題為一次函數的綜合應用,涉及函數與坐標軸的交點、三角形的面積、全等三角形的性質、角平分線的性質定理及分類討論思想等知識.在(1)中注意求函數圖象與坐標軸交點的方法,在(2)中注意分兩種情況,在(3)中注意全等三角形的對應邊相等,在(4)中利用角平分線的性質定理求得關于OG的等式是解題的關鍵.本題考查知識點較多,綜合性很強,但難度不大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:選擇題
 已知△ABC和△DEF關于點O對稱,相應的對稱點如圖所示,則下列結論正確的是( )
已知△ABC和△DEF關于點O對稱,相應的對稱點如圖所示,則下列結論正確的是( )| A. | AO=BO | B. | BO=EO | ||
| C. | 點A關于點O的對稱點是點D | D. | 點D 在BO的延長線上 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -$\sqrt{16}$=-4 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | D. | $\root{3}{(-4)^{2}}$=-4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,一次函數y=kx+b(k≠0)和反比例函數y=$\frac{m}{x}$(m≠0)交于點A(4,1)與點B(-1,n).
如圖,一次函數y=kx+b(k≠0)和反比例函數y=$\frac{m}{x}$(m≠0)交于點A(4,1)與點B(-1,n).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,網格線的交點叫格點,格點P是∠AOB的邊OB上的一點(請利用網格作圖,保留作圖痕跡).
如圖,網格線的交點叫格點,格點P是∠AOB的邊OB上的一點(請利用網格作圖,保留作圖痕跡).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com