
 如圖,一次函數y=kx+b(k≠0)和反比例函數y=$\frac{m}{x}$(m≠0)交于點A(4,1)與點B(-1,n).
如圖,一次函數y=kx+b(k≠0)和反比例函數y=$\frac{m}{x}$(m≠0)交于點A(4,1)與點B(-1,n).分析 (1)把點A(4,1)與點B(-1,n)代入反比例函數y=$\frac{m}{x}$得到m=4,即反比例函數的解析式為y=$\frac{4}{x}$,把點A(4,1)與點B(-1,-4)代入一次函數y=kx+b,得到$\left\{\begin{array}{l}{1=4k+b}\\{-4=-k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$得到一次函數解析式為y=x-3;
(2)根據三角形的面積公式即可得到結論;
(3)由圖象即可可得結論.
解答 (1)解:∵點A(4,1)與點B(-1,n)在反比例函數y=$\frac{m}{x}$(m≠0)圖象上,
∴m=4,即反比例函數的解析式為y=$\frac{4}{x}$,
當x=1時,n=-4,即B(-1,-4),
∵點A(4,1)與點B(-1,-4)在一次函數y=kx+b(k≠0)圖象上,
∴$\left\{\begin{array}{l}{1=4k+b}\\{-4=-k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$
∴一次函數解析式為y=x-3;
(2)解:對于y=x-3,當y=0時,x=3,
∴C(3,0)
∴S△AOB=S△AOC+S△BOC=$\frac{15}{2}$;
(3)解:由圖象可得,當-1<x<0或x>4時,一次函數的值大于反例函數的值.
點評 本題考查的是反比例函數與一次函數的交點問題及三角形的面積公式,熟知坐標軸上點的坐標特點是解答此題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
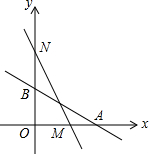 如圖,直線L:y=-$\frac{1}{2}$x+2與x軸、y軸分別交于A、B兩點,在y軸上有一點N(0,4),動點M從A點以每秒1個單位的速度勻速沿x軸向左移動.
如圖,直線L:y=-$\frac{1}{2}$x+2與x軸、y軸分別交于A、B兩點,在y軸上有一點N(0,4),動點M從A點以每秒1個單位的速度勻速沿x軸向左移動.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 河上有一座橋孔為拋物線形的拱橋,水面寬為6米時,水面離橋孔頂部3米.把橋孔看成一個二次函數的圖象,以橋孔的最高點為原點,過原點的水平線為橫軸,過原點的鉛垂線為縱軸,建立如圖所示的平面直角坐標系.
河上有一座橋孔為拋物線形的拱橋,水面寬為6米時,水面離橋孔頂部3米.把橋孔看成一個二次函數的圖象,以橋孔的最高點為原點,過原點的水平線為橫軸,過原點的鉛垂線為縱軸,建立如圖所示的平面直角坐標系.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=(x-1)2+2 | B. | y=(x+1)2+4 | C. | y=(x-1)2-2 | D. | y=(x+2)2-2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com