
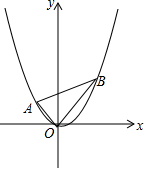
 如圖,二次函數y=$\frac{2}{3}$x2-$\frac{1}{3}$x,圖象過△ABC三個頂點,其中A(-1,m),B(n,n)
如圖,二次函數y=$\frac{2}{3}$x2-$\frac{1}{3}$x,圖象過△ABC三個頂點,其中A(-1,m),B(n,n)分析 (1)先根據二次函數圖象上點的坐標特征,把A(-1,m),B(n,n)分別代入拋物線解析式可求出m和n的值,則得到A(-1,1),B(2,2);
(2)利用待定系數法求出直線AB的解析式,則可確定C點坐標,于是可根據三角形面積公式計算△AOB的面積
解答 解:(1)把A(-1,m)代入y=$\frac{2}{3}$x2-$\frac{1}{3}$x得m=$\frac{2}{3}$+$\frac{1}{3}$=1,則A(-1,1),
把B(n,n)代入y=$\frac{2}{3}$x2-$\frac{1}{3}$x得$\frac{2}{3}$n2-$\frac{1}{3}$n=n,解得n1=0(舍去),n2=2,則B(2,2);
(2)設直線AB的解析式為y=kx+b,
把A(-1,1),B(2,2)分別代入得$\left\{\begin{array}{l}{-k+b=1}\\{2k+b=2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
所以直線AB的解析式為y=$\frac{1}{3}$x+$\frac{4}{3}$,
當x=0時,y=$\frac{1}{3}$x+$\frac{4}{3}$=$\frac{4}{3}$,則C點坐標為(0,$\frac{4}{3}$),
所以△AOB的面積=△AOC的面積+△BOC的面積=$\frac{1}{2}$×$\frac{4}{3}$×(1+2)=2.
點評 本題考查了二次函數圖象上點的坐標特征:二次函數圖象上點的坐標滿足其解析式.也考查了三角形面積公式和待定系數法一次函數解析式.


 高效智能課時作業系列答案
高效智能課時作業系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖,在四邊形ABCD中,∠ABC=∠ADC=90°,點E是AC的中點.(1)求證:△BED是等腰三角形:
已知:如圖,在四邊形ABCD中,∠ABC=∠ADC=90°,點E是AC的中點.(1)求證:△BED是等腰三角形:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 第1排的座位數 | 第2排的座位數 | 第3排的座位數 | 第4排的座位數 | … | 第n排的座位數 |
| 14 | 14+a | 14+2a | 14+3a | … | 14+(n-1)a |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com