
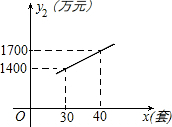
 某企業生成一種節能產品,投放市場供不應求.若該企業每月的產量保持在一定的范圍,每套產品的生產成本不高于50萬元,每套產品的售價不低于120萬元.已知這種產品的月產量x(套)與每套的售價y1(萬元)之間滿足關系式y1=190-2x.月產量x(套)與生成總成本y2(萬元)存在如圖所示的函數關系.
某企業生成一種節能產品,投放市場供不應求.若該企業每月的產量保持在一定的范圍,每套產品的生產成本不高于50萬元,每套產品的售價不低于120萬元.已知這種產品的月產量x(套)與每套的售價y1(萬元)之間滿足關系式y1=190-2x.月產量x(套)與生成總成本y2(萬元)存在如圖所示的函數關系.分析 (1)根據題意可以設出y2與x之間的函數關系式,然后根據圖象中的數據即可求得函數的解析式;
(2)根據題意可以列出相應的不等式組,從而可以求得x的取值范圍;
(3)根據題意可以得到W與x函數關系式,然后化為頂點式,再根據x的取值范圍,即可求得W的最大值.
解答 解:(1)設y2與x的函數關系式為y2=kx+b,
$\left\{\begin{array}{l}{1400=30k+b}\\{1700=40k+b}\end{array}\right.$,得$\left\{\begin{array}{l}{k=30}\\{b=500}\end{array}\right.$,
∴y2與x之間的函數關系式是y2=30x+500;
(2)由題意可得,
$\left\{\begin{array}{l}{190-2x≥120}\\{\frac{30x+500}{x}≤50}\end{array}\right.$,
解得,25≤x≤35,
即月產量x的取值范圍是25≤x≤35;
(3)由題意可得,
W=x[190-2x-$\frac{30x+500}{x}$]=-2(x-40)2+2700,
∵25≤x≤35,
∴x=35時,W取得最大值,此時W=2650,
即當月產量x(套)為35套時,這種產品的利潤W(萬元)最大,最大利潤是2650萬元.
點評 本題考查二次函數的應用、一次函數的應用,一元一次不等式組的應用,解答此類題目的關鍵是明確題意,找出所求問題需要的條件,利用二次函數的頂點式求函數的最值,注意自變量的取值范圍.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
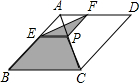 如圖所示,菱形ABCD的對角線的長分別為4和6,P是對角線AC上任一點(點P不與點A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,則陰影部分的面積是6.
如圖所示,菱形ABCD的對角線的長分別為4和6,P是對角線AC上任一點(點P不與點A、C重合),且PE∥BC交AB于E,PF∥CD交AD于F,則陰影部分的面積是6.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
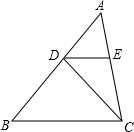 如圖,在△ABC中,AB=4,D是AB上的一點(不與點A、B重合),DE∥BC,交AC于點E,則$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值為$\frac{1}{4}$.
如圖,在△ABC中,AB=4,D是AB上的一點(不與點A、B重合),DE∥BC,交AC于點E,則$\frac{{{S_{△DEC}}}}{{{S_{△ABC}}}}$的最大值為$\frac{1}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
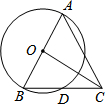 如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD至點C,使得DC=BD,連接AC,OC.若AB=5,BD=$\sqrt{5}$,則OC的長為( )
如圖,AB是⊙O的直徑,BD是⊙O的弦,延長BD至點C,使得DC=BD,連接AC,OC.若AB=5,BD=$\sqrt{5}$,則OC的長為( )| A. | 4 | B. | $\frac{5}{2}$$\sqrt{3}$ | C. | $\frac{9}{5}$$\sqrt{5}$ | D. | $\frac{\sqrt{65}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com