

分析 (1)如圖1中,作EF⊥AB于F.首先證明四邊形BDEF是矩形,再證明在Rt△AEF中,根據tan∠A=$\frac{EF}{AE}$=$\frac{\sqrt{2}}{2}$即可解決問題.
(2)由△ABC∽△EDC,推出$\frac{BC}{DC}$=$\frac{AC}{CE}$,即$\frac{BC}{AC}$=$\frac{DC}{EC}$,推出△ACE∽△BCD,推出$\frac{AE}{BD}$=$\frac{EC}{DC}$,在△EDC中,過點D作DH⊥EC于點H,則EC=2CH,在Rt△CDH中,CH=CD•sin60°=$\frac{\sqrt{3}}{2}$CD,推出EC=$\sqrt{3}$CD,即可解決問題.
(3)只要證明$\frac{AE}{BD}$=$\frac{EC}{DC}$=2sinα,即可,方法類似(2).
解答 解:(1)如圖1中,作EF⊥AB于F.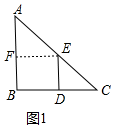
∵∠FBD=∠BDE=∠EFB=90°,
∴四邊形BDEF是矩形,
∴EF=BD,
在Rt△AEF中,∵∠AFE=90°,∠A=45°,
∴tan∠A=$\frac{EF}{AE}$=$\frac{\sqrt{2}}{2}$,
∴AE=$\sqrt{2}$EF,
∴$\frac{AE}{BD}$=$\sqrt{2}$,
故答案為$\sqrt{2}$
(2)如圖2中,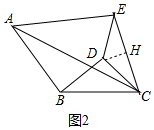
由題意知,△ABC和△EDC都是等腰三角形,且∠ABC=∠EDC=120°,
∴∠ACB=∠CAB=∠ECD=∠CED=30°,
∴△ABC∽△EDC,
∴$\frac{BC}{DC}$=$\frac{AC}{CE}$,即$\frac{BC}{AC}$=$\frac{DC}{EC}$,
又∠ECD+∠DCA=∠ACB+∠DCA,
∴∠DCB=∠ECA,
∴△ACE∽△BCD,
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$,
在△EDC中,過點D作DH⊥EC于點H,則EC=2CH,
在Rt△CDH中,CH=CD•sin60°=$\frac{\sqrt{3}}{2}$CD,
∴EC=$\sqrt{3}$CD.
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$=$\sqrt{3}$.
(3)如圖3中,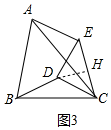
由題意知,△ABC和△EDC都是等腰三角形,且∠ABC=∠EDC=2α,
∴∠ACB=∠CAB=∠ECD=∠CED=90°-α,
∴△ABC∽△EDC,
∴$\frac{BC}{DC}$=$\frac{AC}{CE}$,即$\frac{BC}{AC}$=$\frac{DC}{EC}$,
又∠ECD+∠DCA=∠ACB+∠DCA,
∴∠DCB=∠ECA,
∴△ACE∽△BCD,
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$,
在△EDC中,過點D作DH⊥EC于點H,則EC=2CH,∠CDH=∠HDE=α,
在Rt△CDH中,CH=CD•sinα,
∴EC=2CD•sinα.
∴$\frac{AE}{BD}$=$\frac{EC}{DC}$=2sinα,
故答案為2sinα
點評 本題課程是三角形綜合題、等腰直角三角形的性質、等腰三角形的性質、銳角三角函數、相似三角形的判定和性質等知識,解題的關鍵是靈活運用相似三角形的判定和性質解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
| A. | F+V-E=2 | B. | F+E-V=2 | C. | E+V-F=2 | D. | E-V-F=2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
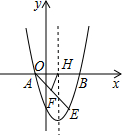 如圖,拋物線y=x2+bx+c經過點A(-1,0),B(3,0).
如圖,拋物線y=x2+bx+c經過點A(-1,0),B(3,0).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
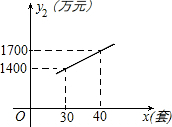 某企業生成一種節能產品,投放市場供不應求.若該企業每月的產量保持在一定的范圍,每套產品的生產成本不高于50萬元,每套產品的售價不低于120萬元.已知這種產品的月產量x(套)與每套的售價y1(萬元)之間滿足關系式y1=190-2x.月產量x(套)與生成總成本y2(萬元)存在如圖所示的函數關系.
某企業生成一種節能產品,投放市場供不應求.若該企業每月的產量保持在一定的范圍,每套產品的生產成本不高于50萬元,每套產品的售價不低于120萬元.已知這種產品的月產量x(套)與每套的售價y1(萬元)之間滿足關系式y1=190-2x.月產量x(套)與生成總成本y2(萬元)存在如圖所示的函數關系.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
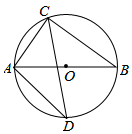 如圖,AB是⊙O的直徑,弦AC=6,BC=8,弦CD平分∠ACB.
如圖,AB是⊙O的直徑,弦AC=6,BC=8,弦CD平分∠ACB.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com