
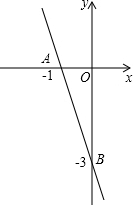
 已知:點A(-1,0),B(0,-3).
已知:點A(-1,0),B(0,-3).分析 (1)根據點A、B的坐標利用待定系數法即可求出直線AB的表達式;
(2)根據平移的性質“上加下減,左加右減”即可得出平移后的直線表達式;
(3)設直線y=-3x-5與x軸交點為點D,與y軸的交點為點C,根據一次函數圖象上點的坐標特征可求出點C、D的坐標,再根據直線AB在第三象限內掃過的圖形面積=S△DOC-S△AOB結合三角形的面積公式即可得出結論.
解答 解:(1)設直線AB的表達式為y=kx+b,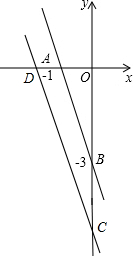
將A(-1,0)、B(0,-3)代入y=kx+b,
$\left\{\begin{array}{l}{-k+b=0}\\{b=-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-3}\\{b=-3}\end{array}\right.$,
∴直線AB的表達式為y=-3x-3.
(2)根據平移的性質可知:直線AB:y=-3x-3向下平移2個單位后得到的直線表達式為y=-3x-3-2=-3x-5.
(3)設直線y=-3x-5與x軸交點為點D,與y軸的交點為點C,
在y=-3x-5中,當x=0時,y=-5,
∴點C的坐標為(0,-5);
當y=-3x-5時,x=-$\frac{5}{3}$,
∴點D的坐標為(-$\frac{5}{3}$,0).
∴直線AB在第三象限內掃過的圖形面積=S△DOC-S△AOB=$\frac{1}{2}$×$\frac{5}{3}$×5-$\frac{1}{2}$×1×3=$\frac{8}{3}$.
點評 本題考查了一次函數圖象與幾何變換、待定系數法求一次函數解析式、一次函數圖象上點的坐標特征以及三角形的面積,解題的關鍵是:(1)根據點的坐標利用待定系數法求出函數表達式;(2)牢記平移的性質“上加下減,左加右減”;(3)結合圖形找出直線AB在第三象限內掃過的圖形面積即為梯形ABCD的面積.


科目:初中數學 來源: 題型:解答題
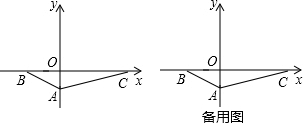
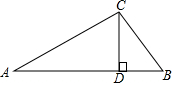 有一種屋頂的截面形狀為三角形(如圖),從屋子的最高處C點立一條垂直于橫梁AB的支柱CD,已知AC=20,BC=15,DB=9,△ABC是直角三角形嗎?說明理由.
有一種屋頂的截面形狀為三角形(如圖),從屋子的最高處C點立一條垂直于橫梁AB的支柱CD,已知AC=20,BC=15,DB=9,△ABC是直角三角形嗎?說明理由.查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
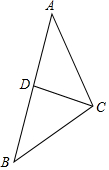 如圖,已知在△ABC中,D為AB的中點,按要求完成下列各小題(保留作圖痕跡,不要求寫作法)
如圖,已知在△ABC中,D為AB的中點,按要求完成下列各小題(保留作圖痕跡,不要求寫作法)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
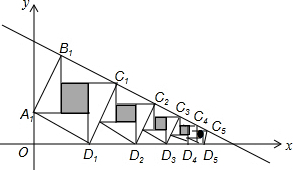 趙爽弦圖是由四個全等的直角三角形與中間的一個小正方形拼成的一個大正方形,如圖所示,若這四個全等直角三角形的兩條直角邊分別平行于x軸和y軸,大正方形的頂點B1、C1、C2、C3、…、Cn在直線y=-$\frac{1}{2}$x+$\frac{7}{2}$上,頂點D1、D2、D3、…、Dn在x軸上,則第n個陰影小正方形的面積為$({\frac{2}{3})}^{2n-2}$.
趙爽弦圖是由四個全等的直角三角形與中間的一個小正方形拼成的一個大正方形,如圖所示,若這四個全等直角三角形的兩條直角邊分別平行于x軸和y軸,大正方形的頂點B1、C1、C2、C3、…、Cn在直線y=-$\frac{1}{2}$x+$\frac{7}{2}$上,頂點D1、D2、D3、…、Dn在x軸上,則第n個陰影小正方形的面積為$({\frac{2}{3})}^{2n-2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com