
分析 (1)由題目中所給和諧點對的定義可知P、Q即為關于原點對稱的兩個點,在反比例函數圖象上找出兩點即可;
(2)①由A、B為和諧點對可求得點B的坐標,則可得到關于m、n的方程組,可求得其值;②當M在x軸上方時,可先求得∠AMB為直角時對應的M點的坐標,當點M向上運動時滿足∠AMB為銳角;當點M在x軸下方時,同理可求得b的取值范圍.
解答 解:
(1)∵y=$\frac{1}{x}$,
∴可取[P(1,1),Q(-1,-1)];
(2)①∵A(2,4)且A和B為和諧點對,
∴B點坐標為(-2,-4),
將A和B兩點坐標代入y=x2+mx+n,可得$\left\{{\begin{array}{l}{4+2m+n=4}\\{4-2m+n=-4}\end{array}}\right.$,
∴$\left\{{\begin{array}{l}{m=2}\\{n=-4}\end{array}}\right.$;
②(ⅰ) M點在x軸上方時,
若∠AMB 為直角(M點在x軸上),則△ABC為直角三角形,
∵A(2,4)且A和B為和諧點對,
∴原點O在AB線段上且O為AB中點,
∴AB=2OA,
∵A(2,4),
∴OA=$2\sqrt{5}$,
∴AB=$4\sqrt{5}$,
在Rt△ABC中,
∵O為AB中點
∴MO=OA=$2\sqrt{5}$,
若∠AMB 為銳角,則$b>2\sqrt{5}$;
(ⅱ) M點在x軸下方時,同理可得,$b<-2\sqrt{5}$,
綜上所述,b的取值范圍為$b>2\sqrt{5}$或$b<-2\sqrt{5}$.
點評 本題為反比例函數的綜合應用,涉及中心對稱、待定系數法、直角三角形的性質、方程思想及分類討論思想等知識.在(1)中理解題目中所給的和諧點對的實質是關于原點對稱的兩個點是解題的關鍵,在(2)①中利用和諧點對的定義求得點B的坐標是解題的關鍵,在(2)②中求得使∠AMB為直角時點M的坐標是解題的關鍵.本題考查知識點較多,綜合性較強,難度適中.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
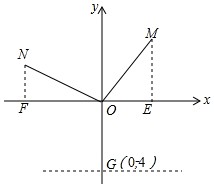 如圖,在直角坐標系中,已知點M(2,3),連接OM,在第二象限作N,使ON⊥OM且ON=OM,y軸上有一點G(0,-4),過G作x軸的平行線l.
如圖,在直角坐標系中,已知點M(2,3),連接OM,在第二象限作N,使ON⊥OM且ON=OM,y軸上有一點G(0,-4),過G作x軸的平行線l.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
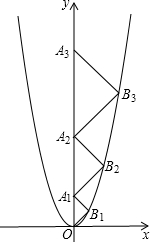 如圖,在平面直角坐標系xOy中,點A1,A2,A3,…,An在y軸的正半軸上,點B1,B2,B3,…,Bn在二次函數y=x2位于第一象限的圖象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,則:
如圖,在平面直角坐標系xOy中,點A1,A2,A3,…,An在y軸的正半軸上,點B1,B2,B3,…,Bn在二次函數y=x2位于第一象限的圖象上,若△OB1A1,△A1B2A2,△A2B3A3,…,△An-1BnAn都是等腰直角三角形,其中∠B1=∠B2=∠B3=…=∠Bn=90°,則:查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 柑橘總質量n/Kg | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
| 損壞柑橘質量m/Kg | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.51 |
| 柑橘損壞的頻率$\frac{m}{n}$ (結果保留小數點后三位) | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,等腰直角三角形ABC中,AB=4cm.點D是BC邊上的動點,以AD為直角邊作等腰直角三角形ADE.在點D從點B移動至點C的過程中,點E移動的路線長為4$\sqrt{2}$cm.
如圖,等腰直角三角形ABC中,AB=4cm.點D是BC邊上的動點,以AD為直角邊作等腰直角三角形ADE.在點D從點B移動至點C的過程中,點E移動的路線長為4$\sqrt{2}$cm.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m<2 | B. | m>2 | C. | m≤2 | D. | m≥2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com