
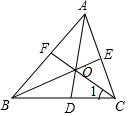
 如圖,△ABC的三條角平分線AD、BE、CF交于點O.
如圖,△ABC的三條角平分線AD、BE、CF交于點O.分析 (1)利用角平分線的定義,得出∠2=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠BAC,∠1=$\frac{1}{2}$∠ACB,再根據(jù)∠AOE是△AOB的外角,得出∠AOE=∠2+∠3,據(jù)此進行計算,即可得出AOE+∠1=90°;
(2)利用三角形的內(nèi)角和定理,以及角平分線的定義,用∠ACB表示出∠AOE,則∠BOD即可得到,然后在直角△OCH中,利用直角三角形的兩個內(nèi)角互余以及角平分線的定義,即可利用∠ACB表示出∠COH,從而證得結(jié)論.
解答 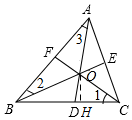 解:(1)∠AOE和∠1之間的關(guān)系:∠AOE+∠1=90°.
解:(1)∠AOE和∠1之間的關(guān)系:∠AOE+∠1=90°.
理由:∵AD、BE、CF都是△ABC的角平分線,
∴∠2=$\frac{1}{2}$∠ABC,∠3=$\frac{1}{2}$∠BAC,∠1=$\frac{1}{2}$∠ACB,
∵∠AOE是△AOB的外角,
∴∠AOE=∠2+∠3
=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠BAC
=$\frac{1}{2}$(∠ABC+∠BAC)
=$\frac{1}{2}$(180°-∠ACB)
=90°-$\frac{1}{2}$∠ACB
=90°-∠1,
∴∠AOE+∠1=90°;
(2)證明:過點O作BC的垂線段,交BC于點H,
∵∠AEO=∠EBC+∠ACB=$\frac{1}{2}$∠ABC+∠ACB,
∴∠AOE=180°-(∠DAC+∠AEO)
=180°-[$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC+∠ACB]
=180°-[$\frac{1}{2}$(∠BAC+∠ABC)+∠ACB]
=180°-[$\frac{1}{2}$(180°-∠ACB)+∠ACB]
=180°-[90°+$\frac{1}{2}$∠ACB]
=90°-$\frac{1}{2}$∠ACB,
∴∠BOD=∠AOE=90°-$\frac{1}{2}$∠ACB,
又∵在Rt△OCH中,∠COH=90°-∠OCD=90°-$\frac{1}{2}$∠ACB,
∴∠BOD=∠COH.
點評 本題主要考查了角平分線的定義,三角形的外角的性質(zhì)以及三角形的內(nèi)角和定理,解題時注意運用:三角形內(nèi)角和是180°,三角形的一個外角等于和它不相鄰的兩個內(nèi)角的和.


 永乾教育寒假作業(yè)快樂假期延邊人民出版社系列答案
永乾教育寒假作業(yè)快樂假期延邊人民出版社系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖是某住宅的平面結(jié)構(gòu)示意圖,圖中標注了有關(guān)尺寸(墻體厚度勿略不計,單位:m).
如圖是某住宅的平面結(jié)構(gòu)示意圖,圖中標注了有關(guān)尺寸(墻體厚度勿略不計,單位:m).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
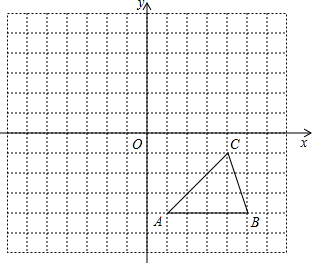 如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點C的坐標為(4,-1).
如圖,方格紙中的每個小方格都是邊長為1個單位的正方形,在建立平面直角坐標系后,△ABC的頂點均在格點上,點C的坐標為(4,-1).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com