
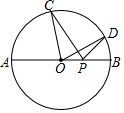
 如圖,已知圓O的面積為3π,AB為圓O的直徑,∠AOC=80°,∠BOD=20°,點P為直徑AB上任意一點,則PC+PD的最小值是3.
如圖,已知圓O的面積為3π,AB為圓O的直徑,∠AOC=80°,∠BOD=20°,點P為直徑AB上任意一點,則PC+PD的最小值是3. 分析 先設圓O的半徑為r,由圓O的面積為3π求出r的值,再作點C關于AB的對稱點C′,連接OC′,DC′,則DC′的長即為PC+PD的最小值,由軸對稱的性質得出∠AOC′的度數,故可得出∠BOC′的度數,再由銳角三角函數的定義即可得出DC′的長.
解答 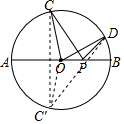 解:設圓O的半徑為r,
解:設圓O的半徑為r,
∵⊙O的面積為3π,
∴3π=πr2,即r=$\sqrt{3}$.
作點C關于AB的對稱點C′,連接OC′,DC′,則DC′的長即為PC+PD的最小值,
∵∠AOC=80°,
∴∠AOC=∠AOC′=80°,
∴∠BOC′=100°,
∵∠BOD=20°,
∴∠DOC′=∠BOC′+∠BOD=100°+20°=120°,
∵OC′=OD,
∴∠ODC′=30°
∴DC′=2OD•cos30°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,即PC+PD的最小值為3.
故答案為:3.
點評 本題考查的是圓周角定理及軸對稱-最短路線問題,根據題意作出點C關于直線AB的對稱點是解答此題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\root{3}{125}$ | B. | -32 | C. | $\sqrt{16}$ | D. | $\sqrt{\frac{1}{4}}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 某滑雪場舉辦冰雪嘉年華活動,采用直升機航拍技術拍攝活動盛況,如圖,通過直升機的鏡頭C觀測到水平雪道一端A處的俯角為30°,另一端B處的俯角為45°.若直升機鏡頭C處的高度CD為300米,點A、D、B在同一直線上,則雪道AB的長度為( )
某滑雪場舉辦冰雪嘉年華活動,采用直升機航拍技術拍攝活動盛況,如圖,通過直升機的鏡頭C觀測到水平雪道一端A處的俯角為30°,另一端B處的俯角為45°.若直升機鏡頭C處的高度CD為300米,點A、D、B在同一直線上,則雪道AB的長度為( )| A. | 300米 | B. | 1502米 | C. | 900米 | D. | (300$\sqrt{3}$+300)米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com