
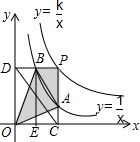
 兩個反比例函數y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限內的圖象如圖所示,點P在y=$\frac{k}{x}$(的圖象上,PC⊥x軸于點C,交y=$\frac{1}{x}$的圖象于點A,PD⊥y軸于點D,交y=$\frac{1}{x}$的圖象于點B,BE⊥x軸于點E,當點P在y=$\frac{k}{x}$(的圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④△OBA的面積等于四邊形
兩個反比例函數y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限內的圖象如圖所示,點P在y=$\frac{k}{x}$(的圖象上,PC⊥x軸于點C,交y=$\frac{1}{x}$的圖象于點A,PD⊥y軸于點D,交y=$\frac{1}{x}$的圖象于點B,BE⊥x軸于點E,當點P在y=$\frac{k}{x}$(的圖象上運動時,以下結論:①BA與DC始終平行;②PA與PB始終相等;③四邊形PAOB的面積不會發生變化;④△OBA的面積等于四邊形分析 ①正確.只要證明$\frac{BD}{PD}$=$\frac{AC}{PC}$即可;
②錯誤.只有當四邊形OCPD為正方形時滿足PA=PB;
③正確.由于矩形OCPD、三角形ODB、三角形OCA為定值,則四邊形PAOB的面積不會發生變化;
④正確.只要證明△OBA的面積=矩形OCPD的面積-S△ODB-S△BAP-S△AOC,四邊形ACEB的面積=矩形OCPD的面積-S△ODB-S△BAP-S△OBE即可.
解答 解:①正確.∵A、B在y=$\frac{1}{x}$上,
∴S△AOC=S△BOE,
∴$\frac{1}{2}$•OC•AC=$\frac{1}{2}$•OE•BE,
∴OC•AC=OE•BE,
∵OC=PD,BE=PC,
∴PD•AC=DB•PC,
∴$\frac{BD}{PD}$=$\frac{AC}{PC}$,
∴AB∥CD.故此選項正確.
②錯誤,不一定,只有當四邊形OCPD為正方形時滿足PA=PB;
③正確,由于矩形OCPD、三角形ODB、三角形OCA為定值,則四邊形PAOB的面積不會發生變化; 故此選項正確.
故此選項正確.
④正確.∵△ODB的面積=△OCA的面積=$\frac{k}{2}$,
∴△ODB與△OCA的面積相等,同理可得:S△ODB=S△OBE,
∵△OBA的面積=矩形OCPD的面積-S△ODB-S△BAP-S△AOC,四邊形ACEB的面積=矩形OCPD的面積-S△ODB-S△BAP-S△OBE
∴△OBA的面積=四邊形ACEB的面積,故此選項正確,
故一定正確的是①③④.
故答案為:①③④.
點評 本題考查反比例函數k是幾何意義、矩形的性質、平行線的判定等知識,本題綜合性比較強,屬于中考填空題中的壓軸題.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=5(x-2)2+3 | B. | y=5(x+2)2+3 | C. | y=5(x-2)2-3 | D. | y=5(x+2)2-3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
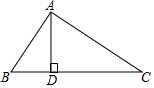 如圖,∠BAC=∠ADB=90°,則下列結論
如圖,∠BAC=∠ADB=90°,則下列結論查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com