
 填空并完成推理過程.
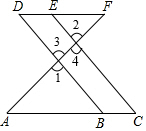
填空并完成推理過程.分析 先證明BD∥CE,然后根據平行線的性質,以及已知條件證明∠D=∠ABD,根據同位角相等,兩直線平行即可證得.
解答  解:∵∠1=∠2,(已知)
解:∵∠1=∠2,(已知)
∠1=∠3(對頂角相等)
∴∠2=∠3,(等量代換)
∴DB∥EC,( 同位角相等,兩直線平行)
∴∠C=∠ABD,( 兩直線平行,同位角相等)
又∵∠C=∠D,(已知)
∴∠D=∠ABD,( 等量代換)
∴AC∥DF.( 內錯角相等,兩直線平行)
故答案為:對頂角相等,DB,EC,同位角相等,兩直線平行,兩直線平行,同位角相等,等量代換,內錯角相等,兩直線平行.
點評 解答此題的關鍵是注意平行線的性質和判定定理的綜合運用.平行線的判定是由角的數量關系判斷兩直線的位置關系,平行線的性質是由平行關系來尋找角的數量關系.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案科目:初中數學 來源: 題型:填空題
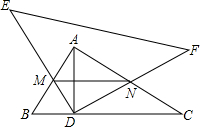 如圖,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC邊上的高,以D為直角頂點的Rt△DEF繞點旋轉,在旋轉過程中,DE、EF分別與邊AB、AC交于點M、N,則線段MN的最大值與最小值的差為$\frac{16}{5}$.
如圖,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,AD是BC邊上的高,以D為直角頂點的Rt△DEF繞點旋轉,在旋轉過程中,DE、EF分別與邊AB、AC交于點M、N,則線段MN的最大值與最小值的差為$\frac{16}{5}$.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
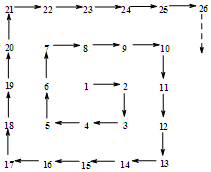 將1開始的自然數,按如圖規律排列,在2、3、5、7、10、13、17、…處分別拐第1、2、3、4、5、6、7、…次彎,則第33次彎出的那一個數是( )
將1開始的自然數,按如圖規律排列,在2、3、5、7、10、13、17、…處分別拐第1、2、3、4、5、6、7、…次彎,則第33次彎出的那一個數是( )| A. | 290 | B. | 226 | C. | 272 | D. | 302 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com