
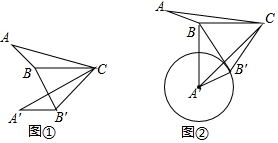
分析 (1)根據(jù)旋轉(zhuǎn)變換的性質(zhì)得到∠A′B′C=∠ABC=130°,∠BCB′=50°,CB=CB′,根據(jù)等腰三角形的性質(zhì)求出∠A′B′B的大小;
(2)(Ⅰ)根據(jù)旋轉(zhuǎn)變換的性質(zhì)求出∠A′B′B=90°,根據(jù)切線的判定定理證明;
(Ⅱ)根據(jù)旋轉(zhuǎn)變換的性質(zhì)和勾股定理計(jì)算即可.
解答 解:(1)由旋轉(zhuǎn)變換的性質(zhì)可知,∠A′B′C=∠ABC=130°,∠BCB′=50°,CB=CB′,
∴∠CB′B=65°,
∴∠A′B′B=∠A′B′C-∠CB′B=65°;
(2)(Ⅰ)直線BB′與⊙A′相切,
∵∠A′B′C=∠ABC=150°,∠BCB′=60°,CB=CB′,
∴∠CB′B=60°,
∴∠A′B′B=∠A′B′C-∠CB′B=90°,
∴直線BB′與⊙A′相切;
(Ⅱ)在Rt△A′B′B中,∠A′B′B=90°,BB′=BC=5,AB′=AB=3,
由勾股定理得,A′B=$\sqrt{AB{′}^{2}+B′{B}^{2}}$=$\sqrt{34}$.
點(diǎn)評(píng) 本題考查的是直線與圓的位置關(guān)系、旋轉(zhuǎn)變換的性質(zhì)、勾股定理的應(yīng)用,掌握切線的判定定理、旋轉(zhuǎn)變換的性質(zhì)是解題的關(guān)鍵.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
 已知:實(shí)數(shù)a,b在數(shù)軸上的位置如圖所示,化簡(jiǎn):$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.
已知:實(shí)數(shù)a,b在數(shù)軸上的位置如圖所示,化簡(jiǎn):$\sqrt{{{({a+1})}^2}}$+$\sqrt{{{({b-1})}^2}}$-|a-b|.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
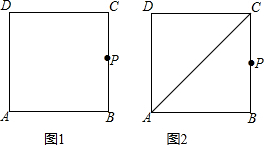
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
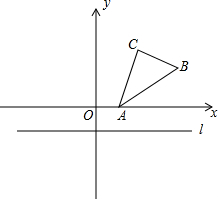 在平面直角坐標(biāo)系中,已知點(diǎn)A(1,0),B(4,2),C(2,3).
在平面直角坐標(biāo)系中,已知點(diǎn)A(1,0),B(4,2),C(2,3).查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com