
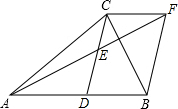
 如圖.在△ABC中.CD是AB邊的中線.E是CD中點,AE=EF.連結BF,CF.
如圖.在△ABC中.CD是AB邊的中線.E是CD中點,AE=EF.連結BF,CF.分析 (1)由SAS證明△AED≌△FEC,得出對應邊相等AD=CF.再由DB=AD,即可得出結論.
(2)由全等三角形的性質得出∠ADE=∠FCE,證出DB∥CF,得出四邊形BDCF是平行四邊形,再由等腰三角形的三線合一性質得出CD⊥AB.即可得出結論;
(3)證明△ABC是等邊三角形,DB=$\frac{1}{2}$AB=1,得出BC=2DB=2,由勾股定理求出CD,即可得出四邊形的面積.
解答 (1)證明:∵CD是AB邊的中線,E是CD中點,
∴AD=DB,DE=CE,
在△AED和△FEC中,$\left\{\begin{array}{l}{AE=EF}&{\;}\\{∠AED=∠FEC}&{\;}\\{DE=CE}&{\;}\end{array}\right.$,
∴△AED≌△FEC(SAS).
∴AD=CF.
∵DB=AD,
∴DB=CF.
(2)解:由(1)得:△AED≌△FEC,
∴∠ADE=∠FCE,
∴DB∥CF,
∵DB=CF,
∴四邊形BDCF是平行四邊形,
∵AC=BC,D是AB的中點,
∴CD⊥AB.
∴∠CDB=90°,
∴四邊形BDCF是矩形.
(3)解:∵∠ABC=60°,AB=2,AC=BC,
∴△ABC是等邊三角形,DB=$\frac{1}{2}$AB=1,
∴BC=2DB=2,
∴CD=$\sqrt{B{C}^{2}-D{B}^{2}}$=$\sqrt{3}$,
∴四邊形BDCF的面積=DB•CD=1×$\sqrt{3}$=$\sqrt{3}$.
點評 本題考查了全等三角形的判定與性質、矩形的判定與性質、等腰三角形的性質、等邊三角形的判定與性質、勾股定理等知識;本題綜合性強,證明三角形全等是解決問題的關鍵.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源:2017屆湖北省襄陽老河口九年級3月月考數學試卷(解析版) 題型:單選題
下列計算正確的是( )
A. (3xy2) 2=6xy4 B. a+2a2=3a3 C. (-x) 7÷(-x) 2=-x5 D. 3x2+4x2=7x4
查看答案和解析>>
科目:初中數學 來源:2017屆江蘇省連云港市灌云縣西片九年級下學期第一次月考數學試卷(解析版) 題型:填空題
某校甲乙兩個體操隊隊員的平均身高相等,甲隊隊員身高的方差是S甲2=1.9,乙隊隊員身高的方差是S乙2=1.2,那么兩隊中隊員身高更整齊的是__隊.(填“甲”或“乙”)
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
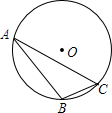 如圖,⊙O的半徑是1,A、B、C是圓周上的三點,∠BAC=36°,則弦BC所對的弧長是$\frac{2}{5}$π或$\frac{8}{5}$π.
如圖,⊙O的半徑是1,A、B、C是圓周上的三點,∠BAC=36°,則弦BC所對的弧長是$\frac{2}{5}$π或$\frac{8}{5}$π.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com