
 已知直角坐標(biāo)系中菱形ABCD中的位置如圖,C、D兩點(diǎn)的坐標(biāo)分別為(4,0),(0,3).現(xiàn)有兩動點(diǎn)P、Q分別從A、C同時出發(fā),點(diǎn)P沿線段AD向終點(diǎn)D運(yùn)動,點(diǎn)Q沿折線CBA向終點(diǎn)A運(yùn)動,P運(yùn)動到D時整個運(yùn)動停止,設(shè)運(yùn)動時間為t秒.
已知直角坐標(biāo)系中菱形ABCD中的位置如圖,C、D兩點(diǎn)的坐標(biāo)分別為(4,0),(0,3).現(xiàn)有兩動點(diǎn)P、Q分別從A、C同時出發(fā),點(diǎn)P沿線段AD向終點(diǎn)D運(yùn)動,點(diǎn)Q沿折線CBA向終點(diǎn)A運(yùn)動,P運(yùn)動到D時整個運(yùn)動停止,設(shè)運(yùn)動時間為t秒.分析 (1)求出OC=4,OD=3,在Rt△COD中,由勾股定理求出CD=5,求出AC=2OC=8,BD=2OD=6,即可求出菱形ABCD的面積($\frac{1}{2}$×AC×BD),根據(jù)S=AD×BE,求出BE即可;
(2)求出AP=t,AQ=10-2t,過點(diǎn)Q作QG⊥AD,垂足為G,根據(jù)△AQG∽△ABE求出QG=$\frac{48}{5}$-$\frac{48}{25}$t,代入S=$\frac{1}{2}$AP•QG求出即可;
(3)當(dāng)t=4秒時,求出AP=4,分兩種情況討論:①當(dāng)點(diǎn)Q在CB上時,只有Q1A=Q1P,過點(diǎn)Q1作Q1M⊥AP,垂足為點(diǎn)M,Q1M交AC于點(diǎn)F,根據(jù)△AMF∽△AOD∽△CQ1F求出FM=$\frac{3}{2}$,Q1F=$\frac{33}{10}$,CQ1=$\frac{4}{3}$QF=$\frac{22}{5}$,由CQ1=4k,求出即可;②當(dāng)點(diǎn)Q在BA上時,存在兩點(diǎn)Q2,Q3,分別使AP=AQ2,PA=PQ3.
Ⅰ、若AP=AQ2,根據(jù)CB+BQ2=10-4=6得出4k=6,求出即可;
Ⅱ、若PA=PQ3,過點(diǎn)P作PN⊥AB,垂足為N,由△ANP∽△AEB,得$\frac{AN}{AE}=\frac{AP}{AB}$,求出AN=$\frac{28}{25}$,AQ3=2AN=$\frac{56}{25}$,求出BC+BQ3=$\frac{194}{25}$,由4k=$\frac{194}{25}$,求出即可
解答 解:(1)∵C,D兩點(diǎn)的坐標(biāo)分別為(4,0),(0,3),
∴OC=4,OD=3,
在Rt△COD中,由勾股定理得:CD=5,
即菱形ABCD的邊長是5,
∵四邊形ABCD是菱形,
∴AD=DC=5,AC⊥BD,AC=2OC=8,BD=2OD=6,
∴菱形ABCD的面積是$\frac{1}{2}$×AC×BD=$\frac{1}{2}$×8×6=24,
∴24=AD×BE,
∴BE=$\frac{24}{5}$;
故答案為:5,24,$\frac{24}{5}$.
(2)由題意,得AP=t,AQ=10-2t,
如圖1,過點(diǎn)Q作QG⊥AD,垂足為G,由QG∥BE得:
△AQG∽△ABE,
∴$\frac{QG}{BE}=\frac{QA}{AB}$,
∴QG=$\frac{48}{5}-\frac{48}{25}$t,
∴S=$\frac{1}{2}$AP•QG=$\frac{1}{2}$•t•($\frac{48}{5}$-$\frac{48}{25}$t),
S=-$\frac{24}{25}$t2+$\frac{24}{5}$t($\frac{5}{2}$≤t≤5);
(3)當(dāng)t=4秒時,
∵點(diǎn)P的速度為每秒1個單位,
∴AP=4,
①當(dāng)點(diǎn)Q在CB上時,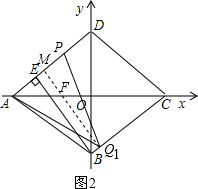
∵PQ≥BE>PA,
∴只存在點(diǎn)Q1,使Q1A=Q1P,
如圖2,過點(diǎn)Q1作Q1M⊥AP,垂足為點(diǎn)M,Q1M交AC于點(diǎn)F,
則AM=$\frac{1}{2}$AP=2,
∵△AMF∽△AOD∽△CQ1F,
∴$\frac{FM}{AM}=\frac{F{Q}_{1}}{C{Q}_{1}}=\frac{OD}{AO}$=$\frac{3}{4}$,
∴FM=$\frac{3}{2}$,
∴Q1F=MQ1-FM=$\frac{33}{10}$,
∴CQ1=$\frac{4}{3}$QF=$\frac{22}{5}$, 由CQ1=4k,
由CQ1=4k,
∴k=$\frac{11}{10}$;
②當(dāng)點(diǎn)Q在BA上時,存在兩點(diǎn)Q2,Q3,分別使AP=AQ2,PA=PQ3.
Ⅰ、若AP=AQ2,如圖3,
CB+BQ2=10-4=6.由4k=6,得k=$\frac{3}{2}$;
Ⅱ、若PA=PQ3,如圖4,
過點(diǎn)P作PN⊥AB,垂足為N,
由△ANP∽△AEB,得$\frac{AN}{AE}=\frac{AP}{AB}$,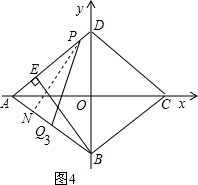 ∵AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{7}{5}$,
∵AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=$\frac{7}{5}$,
∴AN=$\frac{28}{25}$,
∴AQ3=2AN=$\frac{56}{25}$,
∴BC+BQ3=10-$\frac{56}{25}$=$\frac{194}{25}$,由4k=$\frac{194}{25}$,
得k=$\frac{97}{50}$.
綜上所述,當(dāng)t=4秒,使得△APQ為等腰三角形的k的值為$\frac{11}{10}$或$\frac{3}{2}$或$\frac{97}{50}$.
點(diǎn)評 此題是四邊形綜合題,主要考查了相似三角形的性質(zhì)和判定,勾股定理,菱形性質(zhì)的應(yīng)用,查學(xué)生綜合運(yùn)用性質(zhì)進(jìn)行推理和計(jì)算的能力,難度偏大,分類討論思想是解本題的難點(diǎn).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
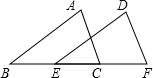 如圖,BE=CF,AB=DE,添加下列哪個條件可以使△ABC≌△DEF( )
如圖,BE=CF,AB=DE,添加下列哪個條件可以使△ABC≌△DEF( )| A. | AC=DF | B. | ∠A=∠D | C. | AC∥DF | D. | BC=EF |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 有兩個不相等的實(shí)數(shù)根 | B. | 有兩個相等的實(shí)數(shù)根 | ||
| C. | 無實(shí)數(shù)根 | D. | 無法確定 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com