
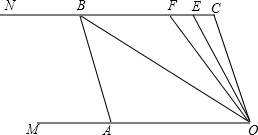
 如圖,已知兩條射線OM∥CN,動線段AB的兩個端點A、B分別在射線OM、CN上,且∠C=∠OAB=108°,點F在線段CB上,OB平分∠AOF,OE平分∠COF.
如圖,已知兩條射線OM∥CN,動線段AB的兩個端點A、B分別在射線OM、CN上,且∠C=∠OAB=108°,點F在線段CB上,OB平分∠AOF,OE平分∠COF.分析 (1)根據兩直線平行,同旁內角互補可得求出∠AOC,再根據平行線的判定方法即可得證;
(2)根據角平分線的性質,即可得解;
(3)根據兩直線平行,內錯角相等可得∠OBC=∠AOB,∠OFC=∠AOF,再根據角平分線的定義可得∠AOF=2∠AOB,從而得到比值不變;
(4)設∠OBA=x,表示出∠OEC,然后利用三角形的內角和定理表示出∠AOB、∠COE,再根據角平分線的定義根據∠AOB+∠COE=$\frac{1}{2}$∠AOC列出方程求解即可.
解答 (1)證明:∵OM∥CN,∠C=∠OAB=108°,
∴∠COA=72°,
則∠BAO+∠AOC=180°,
∴AB∥CO;
(2)解:∵OB平分∠AOF,OE平分∠COF,
∴∠AOB=∠BOF,∠FOE=∠EOC,
∴∠BOE=$\frac{1}{2}$∠AOC=36°;
(3)解:∵OM∥CN,
∴∠OBC=∠AOB,∠OFC=∠AOF,
∵OB平分∠AOF,
∴∠AOF=2∠AOB,
∴∠OFC=2∠OBC,
∴∠OBC:∠OFC=$\frac{1}{2}$;
(4)解:設∠OBA=x,則∠OEC=2x,
在△AOB中,∠AOB=180°-∠OAB-∠ABO=180°-x-108°=72°-x,
在△OCE中,∠COE=180°-∠C-∠OEC=180°-108°-2x=72°-2x,
∵OB平分∠AOF,OE平分∠COF,
∴∠COE+∠AOB=$\frac{1}{2}$∠COF+$\frac{1}{2}$∠AOF=$\frac{1}{2}$∠AOC=$\frac{1}{2}$×72°=36°,
∴72°-x+72°-2x=36°,
解得x=36°,
即∠OBA=36°,
此時,∠OEC=2×36°=72°,
∠COE=72°-2×36°=0°,
點C、E重合,
所以,不存在.
點評 本題考查了平行線的判定與性質,角平分線的定義,解題的關鍵在于性質和判定方法的綜合運用,難點在于(4)根據角度之間的關系列出方程.


 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案科目:初中數學 來源: 題型:選擇題
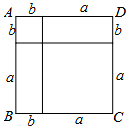 如圖,根據計算正方形ABCD的面積,可以說明下列哪個等式成立( )
如圖,根據計算正方形ABCD的面積,可以說明下列哪個等式成立( )| A. | (a-b)2=a2-2ab+b2 | B. | (a+b)2=a2+2ab+b2 | C. | (a+b)(a-b)=a2-b2 | D. | a(a-b)=a2-ab |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
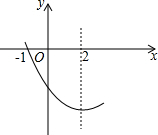 拋物線y=ax2+bx+c(a≠0)圖象的一部分如圖所示,其對稱軸為x=2,與x軸的一個交點是(-1,0),有以下結論:①abc>0;②4a-2b+c<0;③4a+b=0④拋物線與x軸的另一個交點是(5,0)⑤若點(-3,y1)(-6,y2)都在拋物線上,則y1<y2.其中正確的是①③④⑤.(只填序號)
拋物線y=ax2+bx+c(a≠0)圖象的一部分如圖所示,其對稱軸為x=2,與x軸的一個交點是(-1,0),有以下結論:①abc>0;②4a-2b+c<0;③4a+b=0④拋物線與x軸的另一個交點是(5,0)⑤若點(-3,y1)(-6,y2)都在拋物線上,則y1<y2.其中正確的是①③④⑤.(只填序號)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2a-3 | B. | 2a+3 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
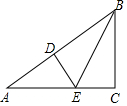 如圖,在△ABC中,∠C=90°,其三邊的長之比為3:4:5,按圖中的方法將它對折,使折痕(圖中虛線)過其中的一個頂點,且使該頂點所在兩邊重合,若不重疊的部分△ADE的面積是6cm2,則△ABC的面積是24或54cm2.
如圖,在△ABC中,∠C=90°,其三邊的長之比為3:4:5,按圖中的方法將它對折,使折痕(圖中虛線)過其中的一個頂點,且使該頂點所在兩邊重合,若不重疊的部分△ADE的面積是6cm2,則△ABC的面積是24或54cm2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com