
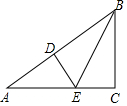
 如圖,在△ABC中,∠C=90°,其三邊的長之比為3:4:5,按圖中的方法將它對折,使折痕(圖中虛線)過其中的一個頂點,且使該頂點所在兩邊重合,若不重疊的部分△ADE的面積是6cm2,則△ABC的面積是24或54cm2.
如圖,在△ABC中,∠C=90°,其三邊的長之比為3:4:5,按圖中的方法將它對折,使折痕(圖中虛線)過其中的一個頂點,且使該頂點所在兩邊重合,若不重疊的部分△ADE的面積是6cm2,則△ABC的面積是24或54cm2. 分析 分兩種情形討論即可:①當BC:AC:AB=3:4:5時,設BC=3k,AC=4k,AB=5k,則BD=BC=3k,AD=2k,設DE=EC=x,在Rt△ADE中,根據AD2+ED2=AE2,得到4k2+x2=(4k-x)2,得到x=$\frac{3}{2}$k,由$\frac{1}{2}$•AD•DE=6,得$\frac{1}{2}$•2k•$\frac{3}{2}$k=6,可得k2=4,再求出△ABC面積即可.②當BC:AC:AB=4:3:5時,設BC=4k,AC=3k,AB=5k,則BD=BC=4k,AD=k,設DE=EC=x,方法類似.
解答 解:①當BC:AC:AB=3:4:5時,
設BC=3k,AC=4k,AB=5k,則BD=BC=3k,AD=2k,設DE=EC=x,
在Rt△ADE中,∵AD2+ED2=AE2,
∴4k2+x2=(4k-x)2,
∴x=$\frac{3}{2}$k,
∵$\frac{1}{2}$•AD•DE=6,
∴$\frac{1}{2}$•2k•$\frac{3}{2}$k=6,
∴k2=4,
∴S△ABC=$\frac{1}{2}$×3k×4k=6k2=24cm2.
②當BC:AC:AB=4:3:5時,設BC=4k,AC=3k,AB=5k,則BD=BC=4k,AD=k,設DE=EC=x,
在Rt△ADE中,∵AD2+ED2=AE2,
∴k2+x2=(3k-x)2,
∴x=$\frac{4}{3}$k,
∵$\frac{1}{2}$•AD•DE=6,
∴$\frac{1}{2}$•k•$\frac{4}{3}$k=6,
∴k2=9,
∴S△ABC=$\frac{1}{2}$×3k×4k=6k2=54cm.
綜上所述,△ABC的面積為24cm2或54cm2.
故答案為24或54.
點評 本題考查翻折變換、直角三角形的性質、勾股定理等知識,解題的關鍵是靈活運用所學知識解決問題,學會用分類討論的思想思考問題,屬于中考常考題型.


 期末集結號系列答案
期末集結號系列答案科目:初中數學 來源: 題型:解答題
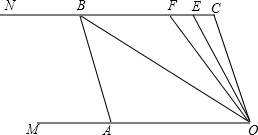 如圖,已知兩條射線OM∥CN,動線段AB的兩個端點A、B分別在射線OM、CN上,且∠C=∠OAB=108°,點F在線段CB上,OB平分∠AOF,OE平分∠COF.
如圖,已知兩條射線OM∥CN,動線段AB的兩個端點A、B分別在射線OM、CN上,且∠C=∠OAB=108°,點F在線段CB上,OB平分∠AOF,OE平分∠COF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 按要求完成下列各題:
按要求完成下列各題:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
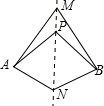 如圖,直線MN是四邊形AMBN的對稱軸,點P是直線MN上的點,下列判斷錯誤的是( )
如圖,直線MN是四邊形AMBN的對稱軸,點P是直線MN上的點,下列判斷錯誤的是( )| A. | AM=BM | B. | ∠ANM=∠BNM | C. | ∠MAP=∠MBP | D. | AP=BN |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 點A在⊙O外 | B. | 點A在⊙O上 | C. | 點A在⊙O內 | D. | 無法確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com