
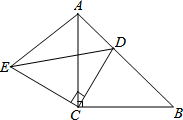
 如圖,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點,求證:
如圖,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點,求證:分析 (1)根據兩邊夾角對應相等的兩個三角形全等即可證明.
(2)只要證明△AED是直角三角形即可解決問題.
解答 證明:(1)∵△ACB和△ECD都是等腰直角三角形
∴∠ACB=∠ECD=90°,AC=BC EC=DC
∴∠ECA=∠DCB,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CD=CE}\end{array}\right.$,
∴△ACE≌△BCD (SAS).
(2)∵△ACE≌△BCD,
∴AE=DB
∴∠EAC=∠B=45°=∠CAB,
∴∠EAD=90°,
∴DE2=AE2+AD2=AD2+DB2.
點評 本題考查全等三角形的判定和性質、勾股定理、等腰直角三角形的性質等知識,解題的關鍵是正確尋找全等三角形解決問題,屬于中考常考題型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
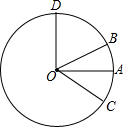 如圖,點A,點B在以點O為圓心的圓上,且∠AOB=30°,如果甲機器人從點A出發沿著圓周按順時針方向以每秒5°的速度行駛,乙機器人從點B出發沿著圓周按逆時針方向行駛,速度是甲機器人的2倍,經過一段時間后,甲、乙分別運動到點C,點D,當乙機器人第一次到達點B時,甲、乙同時停止運動.
如圖,點A,點B在以點O為圓心的圓上,且∠AOB=30°,如果甲機器人從點A出發沿著圓周按順時針方向以每秒5°的速度行駛,乙機器人從點B出發沿著圓周按逆時針方向行駛,速度是甲機器人的2倍,經過一段時間后,甲、乙分別運動到點C,點D,當乙機器人第一次到達點B時,甲、乙同時停止運動.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
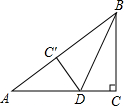 如圖,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,將△BCD沿BD折疊,使點C落在AB邊的C′點,那么△ADC′的面積是6cm2.
如圖,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,將△BCD沿BD折疊,使點C落在AB邊的C′點,那么△ADC′的面積是6cm2.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com