
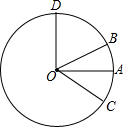
 如圖,點A,點B在以點O為圓心的圓上,且∠AOB=30°,如果甲機器人從點A出發沿著圓周按順時針方向以每秒5°的速度行駛,乙機器人從點B出發沿著圓周按逆時針方向行駛,速度是甲機器人的2倍,經過一段時間后,甲、乙分別運動到點C,點D,當乙機器人第一次到達點B時,甲、乙同時停止運動.
如圖,點A,點B在以點O為圓心的圓上,且∠AOB=30°,如果甲機器人從點A出發沿著圓周按順時針方向以每秒5°的速度行駛,乙機器人從點B出發沿著圓周按逆時針方向行駛,速度是甲機器人的2倍,經過一段時間后,甲、乙分別運動到點C,點D,當乙機器人第一次到達點B時,甲、乙同時停止運動.分析 (1)根據機器人的運動速度,設∠AOC=x°,則∠BOD=2x°,根據角平分線的定義,列出方程即可解答;
(2)根據運動過程中,∠COD=90°,可以分三種情況討論,從而列出方程,解答即可.
解答 解:(1)甲機器人的運動速度每秒為5°,乙機器人的運動速度為每秒10°,
設∠AOC=x°,則∠BOD=2x°,
∵OB是∠COD的平分線,
∴∠BOC=∠BOD=x+30°,
∵∠BOD=2x°,
∴2x=30+x,解得:x=30°.
(2)分三種情況討論:
①當OC,OD運動到如圖1所示的位置時,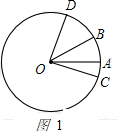
設甲的運動時間為t秒,則∠AOC=5t°,∠BOD=10t°,
∵∠COD=90°,∠AOB=30°,
∴5t+30+10t=90,解得:t=4;
②當OC,OD運動到如圖2所示的位置時,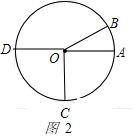
設甲的運動時間為t秒,則∠AOC=5t°,∠BOD=10t°,
∵∠COD=90°,∠AOB=30°,
∴5t+30+10t+90=360,解得:t=16;
③當OC,OD運動到如圖3所示的位置時,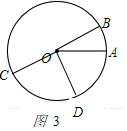
設甲的運動時間為t秒,則∠AOC=5t°,∠BOD=10t°,
∵∠COD=90°,∠AOB=30°,
∴5t+30+10t-90=360,解得:t=28;
答:在機器人運動的整個過程中,若∠COD=90°,甲運動的時間分別為4秒,16秒,28秒.
點評 本題主要考查角的運算中的動點問題及一元一次方程的應用,解決第(2)小題的關鍵是能考慮到各種滿足∠COD的情況.


科目:初中數學 來源: 題型:選擇題
| A. | m-3=0,5m-1=0 | B. | 3-m=0,5m=0 | C. | 5m+1=0,m-3=0 | D. | 5m=0,m-3=0 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
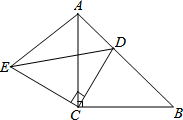 如圖,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點,求證:
如圖,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D為AB邊上一點,求證:查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
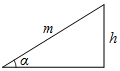 如圖,某游樂場一山頂滑梯的高為h,滑梯的坡角為a,那么滑梯長m為( )
如圖,某游樂場一山頂滑梯的高為h,滑梯的坡角為a,那么滑梯長m為( )| A. | $\frac{h}{sinα}$ | B. | $\frac{h}{tanα}$ | C. | $\frac{h}{cosα}$ | D. | h-sinα |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
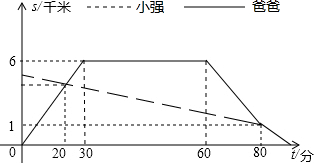 小強的爸爸從家騎自行車去圖書館借書,途中遇到了從圖書館步行回家的小強,爸爸借完書后迅速回家,途中追上了小強,便用自行車載上小強一起回家,結果爸爸比自己單獨騎車回家晚到1分鐘,兩人與家的距離S(千米)和爸爸從家出發后的時間t(分鐘)之間的關系如圖所示.
小強的爸爸從家騎自行車去圖書館借書,途中遇到了從圖書館步行回家的小強,爸爸借完書后迅速回家,途中追上了小強,便用自行車載上小強一起回家,結果爸爸比自己單獨騎車回家晚到1分鐘,兩人與家的距離S(千米)和爸爸從家出發后的時間t(分鐘)之間的關系如圖所示.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com