
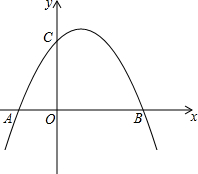
 如圖所示,拋物線y=ax2+x+c(a≠0)與x軸交于點A(-2,0)、點B(6,0),與y軸交于點C.
如圖所示,拋物線y=ax2+x+c(a≠0)與x軸交于點A(-2,0)、點B(6,0),與y軸交于點C.分析 (1)可將A,B兩點的坐標代入函數的解析式中,可求出拋物線的解析式.進而求出對稱軸方程;
(2)四邊形ABDC為等腰梯形可知,C、D縱坐標相等可求得D點坐標,根據A、D坐標用待定系數法可求出直線解析式;
(3)分兩大類共四種情況,第①類P與M的縱坐標相等,第②類P與M的縱坐標互為相反數分別計算,可得P的坐標.
解答 解:(1)根據題意,得$\left\{\begin{array}{l}{4a-2+c=0}\\{36a+6+c=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{c=3}\end{array}\right.$,
故拋物線的解析式為:y=$-\frac{1}{4}{x}^{2}+x+3$,
∵y=$-\frac{1}{4}{x}^{2}+x+3$=$-\frac{1}{4}(x-2)^{2}+4$,
∴對稱軸方程為:x=2;
(2)∵四邊形ABDC為等腰梯形,
∴C、D兩點縱坐標相等,等于3;
在函數:y=$-\frac{1}{4}{x}^{2}+x+3$中當y=3時,有$-\frac{1}{4}{x}^{2}+x+3$=3,
解得:x1=0,x2=4,
故D點坐標為(4,3),
設直線AD的解析式為y=kx+b(k≠0),
∵直線經過點A(-2,0)、點D(4,3),
∴$\left\{\begin{array}{l}{-2k+b=0}\\{4k+b=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=1}\end{array}\right.$,
直線AD的解析式為 $y=\frac{1}{2}x+1$;
(3)存在,
由$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{x=2}\end{array}\right.$,得$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$,
故點M(2,2).
①如圖1,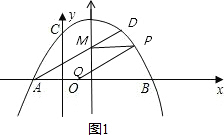
若四邊形AQPM為平行四邊形,則PM∥AQ,即PM∥x軸,
∴P與M的縱坐標相等,
在y=$-\frac{1}{4}{x}^{2}+x+3$中,當y=2時,有$-\frac{1}{4}{x}^{2}+x+3$=2,解得:$x=2±2\sqrt{2}$,
故此時點P坐標為:$(2+2\sqrt{2},2)$或$(2-2\sqrt{2},2)$;
②如圖2,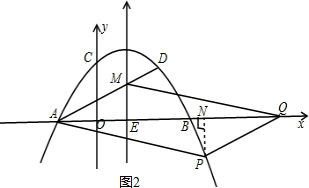
過點P作PN⊥AQ垂足為N,則∠AEM=∠PNQ=90°,
∵四邊形AQPM為平行四邊形,
∴AM=PQ,∠MAE=∠PQN,
在△AME和△QPN中,
∵$\left\{\begin{array}{l}{∠MAE=∠PQN}\\{∠AEM=∠PNQ}\\{AM=QP}\end{array}\right.$,
∴△AME≌△QPN(AAS),
∴ME=PN,
故M、P的縱坐標互為相反數,
在y=$-\frac{1}{4}{x}^{2}+x+3$中,當y=-2時,有$-\frac{1}{4}{x}^{2}+x+3$=-2,解得:$x=2±2\sqrt{6}$,
故此時點P的坐標為:$(2+2\sqrt{6},-2)$或$(2-2\sqrt{6},-2)$;
綜上,點P的坐標為:$(2+2\sqrt{2},2)$、$(2-2\sqrt{2},2)$、$(2+2\sqrt{6},-2)$、$(2-2\sqrt{6},-2)$.
點評 本題主要考查了待定系數法求二次函數解析式及四邊形與二次函數相關綜合知識,分類討論是解題關鍵,找出滿足條件的所有點的坐標是難點.


科目:初中數學 來源: 題型:解答題
 已知拋物線y=x2+bx+c與x軸交于A,B兩點,與y軸交于點C,O是坐標原點,點A的坐標是(-1,0),點C的坐標是(0,-3).在第四象限內的拋物線上有一動點D,過D作DE⊥x軸,垂足為E,交BC于點F.設點D的橫坐標為m.
已知拋物線y=x2+bx+c與x軸交于A,B兩點,與y軸交于點C,O是坐標原點,點A的坐標是(-1,0),點C的坐標是(0,-3).在第四象限內的拋物線上有一動點D,過D作DE⊥x軸,垂足為E,交BC于點F.設點D的橫坐標為m.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知:如圖所示的兩條拋物線的解析式分別是y1=-ax2-ax+1,y2=ax2-ax-1(其中a為常數,且a>0).
已知:如圖所示的兩條拋物線的解析式分別是y1=-ax2-ax+1,y2=ax2-ax-1(其中a為常數,且a>0).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 一個大正方形和四個全等的小正方形按圖①、②兩種方式擺放,則圖②的大正方形中未被小正方形覆蓋部分的面積為( )
一個大正方形和四個全等的小正方形按圖①、②兩種方式擺放,則圖②的大正方形中未被小正方形覆蓋部分的面積為( )| A. | a-b | B. | a+b | C. | ab | D. | a2-ab |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,將邊長為4的正方形ABCD折疊,使B點落在邊AD上,記作B′(不與A、D重合)、EF為折痕,設AB′=x.
如圖,將邊長為4的正方形ABCD折疊,使B點落在邊AD上,記作B′(不與A、D重合)、EF為折痕,設AB′=x.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
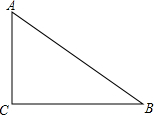 如圖,Rt△ABC中,∠C=90°,AB=5,AC=3,現將△ABC繞著頂點B旋轉,記點C的對應點為點C1,當點A,B,C1三點共線時,求∠BC1C的正切值=3或$\frac{1}{3}$.
如圖,Rt△ABC中,∠C=90°,AB=5,AC=3,現將△ABC繞著頂點B旋轉,記點C的對應點為點C1,當點A,B,C1三點共線時,求∠BC1C的正切值=3或$\frac{1}{3}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,DE是△ABC邊AB的垂直平分線,若BC=8cm,AC=10cm,則△DBC的周長為( )
如圖,DE是△ABC邊AB的垂直平分線,若BC=8cm,AC=10cm,則△DBC的周長為( )| A. | 16cm | B. | 18cm | C. | 30cm | D. | 2cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com