
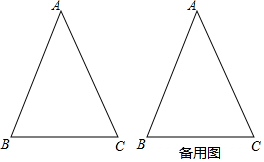
分析 (1)先根據等腰三角形的性質以及旋轉的性質,求得∠A1B1C=∠B=67.5°,再根據平角的定義求得∠AB1A1的度數;
(2)先根據等腰三角形的性質以及旋轉的性質,求得∠A2CB2=∠ACB=67.5°,進而得到∠CB2B=∠B=67.5°,以及∠B2CB=45°,根據角的和差關系得到∠BCA2=112.5°,從而得出∠B+∠BCA2=180°,進而判定AB∥A2C;
(3)先根據等腰三角形的性質以及旋轉的性質,求得∠BAA2+∠B=180°,得出AA2∥BC,再根據AB∥A2C,判定四邊形ABCA2是平行四邊形,進而得出AA2=BC,再根據CB=CB2,可得AA2=B2C,最后根據SAS即可判定△AB2A2≌△B2AC.
解答 解:(1)如圖所示,∵△ABC中,AB=AC,∠BAC=45°,
∴∠B=$\frac{1}{2}$(180°-∠A)=67.5°,
由旋轉可得,∠A1B1C=∠B=67.5°,
∴∠AB1A1=180°-∠A1B1C=112.5°;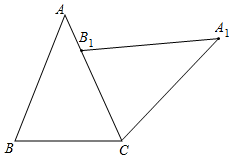
(2)AB∥A2C.
理由:如圖所示,在△ABC中,AB=AC,∠BAC=45°,
∴∠ACB=$\frac{1}{2}$(180°-∠BAC)=67.5°,
由旋轉可得,CB=CB2,∠A2CB2=∠ACB=67.5°,
∴∠CB2B=∠B=67.5°,
∴旋轉角∠B2CB=45°,
∴∠BCA2=45°+67.5°=112.5°,
∴∠B+∠BCA2=180°,
∴AB∥A2C;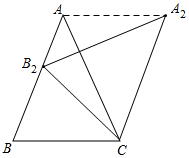
(3)如圖所示,連接AA2,
由(2)可得∠CB2B=∠B=67.5°,
∴∠AB2C=180°-67.5°=112.5°,
由旋轉可得,∠ACA2=∠B2CB=45°,AC=A2C,
∴△ACA2中,∠CAA2=$\frac{1}{2}$(180°-∠ACA2)=67.5°,
∴∠B2AA2=∠BAC+∠CAA2=45°+67.5°=112.5°,
∴∠BAA2+∠B=112.5°+67.5°=180°,且∠B2AA2=∠AB2C,
∴AA2∥BC,
又∵AB∥A2C,
∴四邊形ABCA2是平行四邊形,
∴AA2=BC,
又∵CB=CB2,
∴AA2=B2C,
在△AB2A2和△B2AC中,
$\left\{\begin{array}{l}{A{A}_{2}={B}_{2}C}\\{∠{B}_{2}A{A}_{2}=∠A{B}_{2}C}\\{A{B}_{2}={B}_{2}A}\end{array}\right.$,
∴△AB2A2≌△B2AC(SAS).
點評 本題屬于三角形綜合題,主要考查了等腰三角形的性質,旋轉的性質,全等三角形的判定以及平行四邊形的判定與性質的綜合應用,解決問題的關鍵是掌握旋轉的性質:旋轉前、后的圖形全等.解題時注意:平行四邊形的對邊相等.


 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:初中數學 來源: 題型:解答題
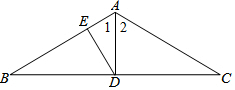 如圖,在△ABC中,∠B=∠C=30°,D是BC邊上的中點,DE⊥AB于E,BC=12.求:
如圖,在△ABC中,∠B=∠C=30°,D是BC邊上的中點,DE⊥AB于E,BC=12.求:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com