

分析 (1)構造全等三角形,由全等三角形對應線段之間的相等關系,求出點D、點E的坐標;
(2)利用待定系數法求出拋物線的解析式;
(3)①為求s的表達式,需要識別正方形(與拋物線)的運動過程.正方形的平移,從開始到結束,總共歷時$\frac{3}{2}$秒,期間可以劃分成三個階段:當0<t≤$\frac{1}{2}$時,對應圖a;當$\frac{1}{2}$<t≤1時,對應圖b;當1<t≤$\frac{3}{2}$時,對應圖c;
②當運動停止時,點E到達y軸,點E(-3,2)運動到點E′(0,$\frac{7}{2}$),可知正方形BCDE在y軸上所截得的線段的中點運動的路線長為CE'的長;整條拋物線向右平移了3個單位,向上平移了$\frac{3}{2}$個單位,由此得到平移之后的拋物線解析式,進而求出其頂點坐標.
解答 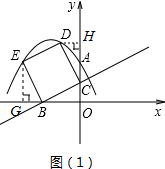 解:(1)由題意可知:OB=2,OC=1.
解:(1)由題意可知:OB=2,OC=1.
如圖(1)所示,過D點作DH⊥y軸于H,過E點作EG⊥x軸于G.
易證△CDH≌△BCO,
∴DH=OC=1,CH=OB=2,
∴D(-1,3);
同理可得△EBG≌△BCO,
∴BG=OC=1,EG=OB=2,
∴E(-3,2).
故答案為:(-1,3),(-3,2).
(2)拋物線經過(0,2)、(-1,3)、(-3,2),
則$\left\{\begin{array}{l}{c=2}\\{a-b+c=3}\\{9a-3b+c=2}\end{array}\right.$,
解得 $\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=-\frac{3}{2}}\\{c=2}\end{array}\right.$,
∴y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2.
(3)①當點D運動到y軸上時,t=$\frac{1}{2}$.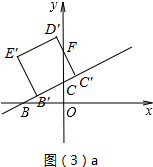
當0<t≤$\frac{1}{2}$時,如圖(3)a所示.
設D′C′交y軸于點F,
∵tan∠BCO=$\frac{OB}{OC}$=2,
又∵∠BCO=∠FCC′,
∴tan∠FCC′=2,即$\frac{FC'}{CC'}$=2,
∵CC′=$\sqrt{5}$t,
∴FC′=2$\sqrt{5}$t.?
∴S△CC′F?=$\frac{1}{2}$CC′•FC′=$\frac{1}{2}$$\sqrt{5}$t×2$\sqrt{5}$t=5t2
當點B運動到點C時,t=1.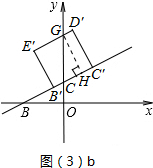
當$\frac{1}{2}$<t≤1時,如圖(3)b所示.
設D′E′交y軸于點G,過G作GH⊥B′C′于H.
在Rt△BOC中,BC=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴GH=$\sqrt{5}$,
∴CH=$\frac{1}{2}$GH=$\frac{1}{2}$$\sqrt{5}$,
∵CC′=$\sqrt{5}$t,
∴HC′=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$,
∴GD′=$\sqrt{5}$t-$\frac{\sqrt{5}}{2}$,
∴S梯形CC′D′G?=$\frac{1}{2}$($\sqrt{5}$t-$\frac{\sqrt{5}}{2}$+$\sqrt{5}$t) $\sqrt{5}$=5t-$\frac{5}{4}$,
當點E運動到y軸上時,t=$\frac{3}{2}$.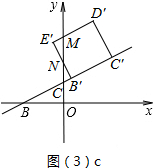
當1<t≤$\frac{3}{2}$時,如圖(3)c所示,
設D′E′、E′B′分別交y軸于點M、N,
∵CC′=$\sqrt{5}$t,B′C′=$\sqrt{5}$,
∴CB′=$\sqrt{5}$t-$\sqrt{5}$,
∴B′N=2CB′=2$\sqrt{5}$t-2$\sqrt{5}$,
∵B′E′=$\sqrt{5}$,
∴E′N=B′E′-B′N=3$\sqrt{5}$-2$\sqrt{5}$t,
∴E′M=$\frac{1}{2}$E′N=$\frac{1}{2}$(3$\sqrt{5}$-2$\sqrt{5}$t),
∴S△MNE′=$\frac{1}{2}$(3$\sqrt{5}$-2$\sqrt{5}$t)•$\frac{1}{2}$(3$\sqrt{5}$-2$\sqrt{5}$t)=5t2-15t+$\frac{45}{4}$,
∴S五邊形B′C′D′MN?=S正方形B′C′D′E′?-S△MNE′?=$(\sqrt{5})^{2}$-(5t2-15t+$\frac{45}{4}$)=-5t2+15t-$\frac{25}{4}$,
綜上所述,S與x的函數關系式為:
當0<t≤$\frac{1}{2}$時,S=5t2;
當$\frac{1}{2}$<t≤1時,S=5t-$\frac{5}{4}$;
當1<t≤$\frac{3}{2}$時,S=-5t2+15t-$\frac{25}{4}$;
②當點E運動到點E′時,運動停止.如圖(3)d所示,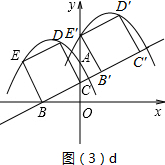
正方形BCDE在y軸上所截得的線段的中點運動的路線長為CE'的長,
∵∠CB′E′=∠BOC=90°,∠BCO=∠B′CE′,
∴△BOC∽△E′B′C,
∴$\frac{OB}{B'E'}$=$\frac{BC}{E'C}$,
∵OB=2,B′E′=BC=$\sqrt{5}$,
∴$\frac{2}{\sqrt{5}}$=$\frac{\sqrt{5}}{E'C}$,
∴CE′=$\frac{5}{2}$,即正方形BCDE在y軸上所截得的線段的中點運動的路線長為$\frac{5}{2}$,
∴OE′=OC+CE′=1+$\frac{5}{2}$=$\frac{7}{2}$,
∴E′(0,$\frac{7}{2}$),
由點E(-3,2)運動到點E′(0,$\frac{7}{2}$),可知整條拋物線向右平移了3個單位,向上平移了$\frac{3}{2}$個單位.
∵y=-$\frac{1}{2}$x2-$\frac{3}{2}$x+2=-$\frac{1}{2}$(x+$\frac{3}{2}$)2+$\frac{25}{8}$,
∴原拋物線頂點坐標為(-$\frac{3}{2}$,$\frac{25}{8}$),
∴運動停止時,拋物線的頂點坐標為($\frac{3}{2}$,$\frac{37}{8}$).
故答案為:$\frac{5}{2}$,($\frac{3}{2}$,$\frac{37}{8}$).
點評 本題是二次函數綜合題,主要考查了二次函數的圖象與性質、待定系數法求解析式、拋物線與幾何變換(平移)、相似三角形的判定與性質、全等三角形的判定與性質、正方形的性質等的綜合應用.難點在于第(3)問,識別正方形和拋物線平移過程的不同階段是解決問題的關鍵所在.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.
如圖,邊長為2的菱形ABCD中,∠BAD=60°,現有∠BFE=30°的三角板△BEF,將△BEF繞B旋轉得△BE′F′,BE′,BF′所在直線分別交線段AC于點M,N,若點C關于直線BE′的對稱點為C′,當C′N⊥AC時,AN的長為$\sqrt{3}$-1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
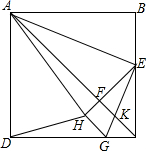 如圖所示,在邊長為10的正方形ABCD中,AC是對角線,點E,G分別是邊BC,CD上的點,將△ABE沿AE折疊得到△AFE,且F恰好落在對角線AC上,同理將△CEG沿GE折疊得到△HEG,使得EH與EF重合,連接AH,DH.
如圖所示,在邊長為10的正方形ABCD中,AC是對角線,點E,G分別是邊BC,CD上的點,將△ABE沿AE折疊得到△AFE,且F恰好落在對角線AC上,同理將△CEG沿GE折疊得到△HEG,使得EH與EF重合,連接AH,DH.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
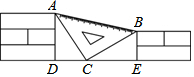 課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),∠ACB=90°,AC=BC,從三角板的刻度可知AB=20cm,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為$\frac{200}{13}$cm.
課間,小聰拿著老師的等腰直角三角板玩,不小心掉到兩墻之間(如圖),∠ACB=90°,AC=BC,從三角板的刻度可知AB=20cm,小聰很快就知道了砌墻磚塊的厚度的平方(每塊磚的厚度相等)為$\frac{200}{13}$cm.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com