Question

3．已知BD、CE分別是△ABC的AC邊、AB邊上的高，M是BC邊的中點，分別聯結MD、ME、DE．

（1）當∠BAC＜90°時，垂足D、E分別落在邊AC、AB上，如圖1，求證：DM=EM．
（2）若∠BAC=135°，試判斷△DEM的形狀，簡寫解答過程．
（3）當∠BAC＞90°時，設∠BAC的度數為x，∠DME的度數為y，求y與x之間的函數關系式．

Answer 1

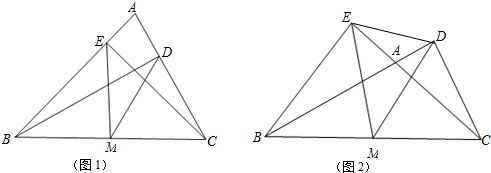
分析 （1）根據已知條件知，MD是Rt△BCD斜邊BC上的中線，ME是Rt△BCE斜邊BC上的中線，所以根據直角三角形斜邊上的中線的性質進行證明即可；
（2）根據等腰三角形的性質得到∠DBM=∠BDM，∠MEC=∠MCE，由三角形的外角的性質得到∠BME=2∠BCE，∠CMD=2∠DBM，根據三角形的內角和得到∠DBC+∠ECM=45°，即可得到結論；
（3）根據等腰三角形的性質得到∠DBM=∠BDM，∠MEC=∠MCE，由三角形的外角的性質得到∠BME=2∠BCE，∠CMD=2∠DBM，根據三角形的內角和得到∠DBC+∠ECM=180°-x，根據平角的定義即可得到結論．

解答 （1）證明：∵BD、CE是△ABC的兩條高，M是BC的中點，
∴在Rt△BDC中，MD是斜邊BC上的中線，
∴MD=$\frac{1}{2}$BC；
同理，得
ME=$\frac{1}{2}$BC，
∴ME=MD；

（2）∵BM=CM=DM=EM，
∴∠DBM=∠BDM，∠MEC=∠MCE，
∴∠BME=2∠BCE，∠CMD=2∠DBM，
∵∠BAC=135°，
∴∠DBC+∠ECM=45°，
∴∠BME+∠CMD=90°，
∴∠DME=90°，
∴△DEM是等腰直角三角形；

（3）∵BM=CM=DM=EM，
∴∠DBM=∠BDM，∠MEC=∠MCE，
∴∠BME=2∠BCE，∠CMD=2∠DBM，
∵∠BAC=x，
∴∠DBC+∠ECM=180°-x，
∴∠BME+∠CMD=360°-2x，
∴∠DME=180°-（∠BME+∠CMD）=2x-180°，
即y=2x-180°．

點評 本題考查了直角三角形斜邊上的中線等于斜邊的一半，等腰直角三角形的判定，三角形的內角和，三角形外角的性質，熟記直角三角形斜邊上的中線等于斜邊的一半是解題的關鍵．