

分析 (1)先根據勾股定理求AC=4,根據平移的性質和平行四邊形的性質得:PQ∥AB,列比例式為$\frac{CP}{CA}$=$\frac{CQ}{CB}$,代入可求t的值;
(2)作輔助線,構建高線,利用面積法求AE的長,利用勾股定理計算CE的長,證明△CPF∽△CAE,列式可表示PF的長,根據面積公式計算y與t之間的函數關系式;
(3)根據同底等高的兩個三角形面積相等得:S△PQC=S△MQC,由已知得:S△MQC:S△ABC=1:5,把(2)中的式子代入可求t的值;
(4)如圖2,證明△MQP∽△PFQ,列比例式可求得:PQ2=PM×FQ,由勾股定理相結合得:PF2+FQ2=PM×FQ,代入列方程可得結論.
解答 解:(1)在Rt△ABC中,由勾股定理得,
AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=4,
由平移性質可得MN∥AB;
∵PQ∥MN,
∴PQ∥AB,
∴$\frac{CP}{CA}$=$\frac{CQ}{CB}$,即$\frac{4-t}{4}$=$\frac{t}{5}$,
解得,t=$\frac{20}{9}$;
(2)如圖2,作PF⊥BC于點F,AE⊥BC于點E,
由S△ABC=$\frac{1}{2}$AB×AC=$\frac{1}{2}$AE×BC可得,$\frac{1}{2}$×3×4=$\frac{1}{2}$×5AE,
∴AE=$\frac{12}{5}$,
由勾股定理得:CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=$\frac{16}{5}$,
∵PF⊥BC,AE⊥BC,
∴AE∥PF,
∴△CPF∽△CAE,
∴$\frac{CP}{CA}$=$\frac{CF}{CE}$=$\frac{PF}{AE}$,即$\frac{4-t}{4}$=$\frac{CF}{\frac{16}{5}}$=$\frac{PF}{\frac{12}{5}}$,
解得,CF=$\frac{16-4t}{5}$,PF=$\frac{12-3t}{5}$,
∵PM∥BC,所以M到BC的距離h=PF=$\frac{12-3t}{5}$,
∴△QCM是面積y=$\frac{1}{2}$CQ×h=$\frac{1}{2}$×t×$\frac{12-3t}{5}$=-$\frac{3}{10}$t2+6t;
(3)∵PM∥BC,
∴S△PQC=S△MQC,
∵S△QMC:S四邊形ABQP=1:4,
∴S△MQC:S△ABC=1:5,
則5(-$\frac{3}{10}$t2+6t)=$\frac{1}{2}$×4×3,
t2-4t+4=0,
解得:t1=t2=2,
∴當t=2時,S△QMC:S四邊形ABQP=1:4;
(4)如圖2,∵PQ⊥MQ,
∴∠MQP=∠PFQ=90°,
∵MP∥BC,
∴∠MPQ=∠PQF,
∴△MQP∽△PFQ,
∴$\frac{PM}{PQ}$=$\frac{PQ}{FQ}$,
∴PQ2=PM×FQ,
即PF2+FQ2=PM×FQ,
由CF=$\frac{16-4t}{5}$,得FQ=CF-CQ=$\frac{16-9t}{5}$,
則($\frac{12-3t}{5}$)2+($\frac{16-9t}{5}$)2=5×$\frac{16-9t}{5}$,
整理得2t2-3t=0,
解得t1=0(舍),t2=$\frac{3}{2}$,
答:當t=$\frac{3}{2}$時,PQ⊥MQ.
點評 本題是四邊形的綜合題,考查了平行四邊形、平移、勾股定理、相似三角形的性質和判定,根據平移的特點,確定等量關系是關鍵,可以利用相似列等量關系,也可以利用已知面積的比列等量關系,解方程可以解決問題.


科目:初中數學 來源: 題型:解答題
 如圖,正方形ABCD的頂點A的坐標為(0,3),頂點B在軸的正方向上,tan∠OBA=3,對角線AC,BD交于點P,射線OP交AB于點N,交DC于點M,點R從O出發沿OM方向以每秒$\sqrt{2}$個單位的速度運動,運動時間為t.
如圖,正方形ABCD的頂點A的坐標為(0,3),頂點B在軸的正方向上,tan∠OBA=3,對角線AC,BD交于點P,射線OP交AB于點N,交DC于點M,點R從O出發沿OM方向以每秒$\sqrt{2}$個單位的速度運動,運動時間為t.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
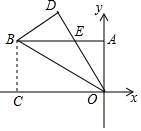 長方形OABC在平面直角坐標系內的位置如圖所示,將長方形沿BO折疊,使點C落在點D處,DO與AB交于點E,BC=4cm,BA=8cm,則點E的坐標為( )
長方形OABC在平面直角坐標系內的位置如圖所示,將長方形沿BO折疊,使點C落在點D處,DO與AB交于點E,BC=4cm,BA=8cm,則點E的坐標為( )| A. | (-3,4) | B. | (-3.5,4) | C. | (-3.7,4) | D. | (-4,4) |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
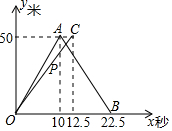 甲、乙兩人在相鄰兩條直跑道上進行競走比賽(注:跑道長50米,兩人均往返一次,返回時轉身的時間忽略不計),圖中的折線OA-AB是甲離出發點的距離y(米)與比賽時間x(秒)的函數圖象;線段OC是乙離出發點的距離y(米)與比賽時間x(秒)的函數圖象,其中x≥0,線段OC與AB相交于點P.根據圖象,解決下列問題:
甲、乙兩人在相鄰兩條直跑道上進行競走比賽(注:跑道長50米,兩人均往返一次,返回時轉身的時間忽略不計),圖中的折線OA-AB是甲離出發點的距離y(米)與比賽時間x(秒)的函數圖象;線段OC是乙離出發點的距離y(米)與比賽時間x(秒)的函數圖象,其中x≥0,線段OC與AB相交于點P.根據圖象,解決下列問題:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com