
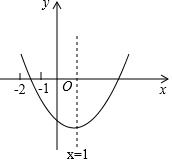
 二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則$\frac{b}{a}$的值為-2;$\frac{c}{a}$的取值范圍為-8<$\frac{c}{a}$<-3.
二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則$\frac{b}{a}$的值為-2;$\frac{c}{a}$的取值范圍為-8<$\frac{c}{a}$<-3. 分析 根據拋物線的對稱軸為x=1可得$\frac{b}{a}$=-2,由當x=-2時y>0,即4a-2b+c>0 ①,當x=-1時y<0,即a-b+c<0 ②,將b=-2a代入可得$\frac{c}{a}$的取值范圍.
解答 解:∵拋物線的對稱軸為直線x=1,
∴x=-$\frac{b}{2a}$=1,即$\frac{b}{a}$=-2;
∵當x=-2時,y>0,即4a-2b+c>0 ①,
當x=-1時,y<0,即a-b+c<0 ②,
將b=-2a代入①、②得:c>-8a,c<-3a,
又∵a>0,
∴-8<$\frac{c}{a}$<-3,
故答案為:-2,-8<$\frac{c}{a}$<-3.
點評 本題考查了拋物線圖象與系數的關系,其中a由拋物線的開口方向決定,a與b同號對稱軸在y軸左邊;a與b異號對稱軸在y軸右邊,c的符合由拋物線與y軸的交點在正半軸或負半軸有關.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:初中數學 來源: 題型:選擇題
| A. | x≠-1 | B. | x≥2 | C. | x≠2 | D. | x≥-1且x≠2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 70° | B. | 30° | C. | 70°或30° | D. | 無法確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優味美,客商聞訊前來采購,經協商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.
我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優味美,客商聞訊前來采購,經協商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 將拋物線y=x2向左平移4個單位后,再向下平移2個單位,則此時拋物線的解析式是y=(x+4)2-2 | |
| B. | 方程x2+2x+3=0有兩個不相等的實數根 | |
| C. | 平行四邊形既是中心對稱圖形又是軸對稱圖形 | |
| D. | 平分弦的直徑垂直于弦,并且平分這條弦所對的兩條弧 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 一、二、三象限 | B. | 一、三、四象限 | C. | 一、二、四象限 | D. | 二、三、四象限 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com