
 我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優味美,客商聞訊前來采購,經協商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.
我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優味美,客商聞訊前來采購,經協商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.分析 (1)分別根據當0<x≤10時,y=2000,當10<x≤20時,設函數關系式為y=kx+b,分別求出即可;
(2)利用當0<x≤10時,老張獲得的利潤為:w=(2000-1200)x,當10<x≤20時,老張獲得的利潤為w=(-80x+28 00-800)x分別求出即可.
解答 解:(1)當0<x≤10時,y=2000.
當10<x≤20時,設BC滿足的函數關系式為y=kx+b,
∴$\left\{\begin{array}{l}{10k+b=2000}\\{20k+b=1200}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-80}\\{b=2800}\end{array}\right.$,
∴y與x之間的函數關系式為:y=-80x+2800.
(2)當0<x≤10時,老張獲得的利潤為:
w=(2000-800)x
=1200x≤12 000,此時老張獲得的最大利潤為12 000元.
當10<x≤20時,老張獲得的利潤為w=(-80x+2800-800)x
=-80(x2-25x)=-80(x-12.5)2+12500.
∴當x=12.5時,利潤w取得最大值,最大值為12500元.
∵12500>12 000,
∴當客商的采購量為12.5噸時,老張在這次買賣中所獲得的利潤最大,最大利潤為12500元.
點評 此題主要考查了二次函數的應用以及分段函數的應用,根據數形結合以及分類討論得出是解題關鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:選擇題
| A. | 該函數的圖象經過點(2,2) | B. | 該函數的圖象位于第一、三象限 | ||
| C. | 當x>0時,y的值隨x的增大而增大 | D. | 當x>-1時,y>4 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 將兩張長方形紙片如圖所示擺放,使其中一張長方形紙片的一個頂點恰好落在另一張長方形紙片的一邊上,則∠1和∠2的關系是( )
將兩張長方形紙片如圖所示擺放,使其中一張長方形紙片的一個頂點恰好落在另一張長方形紙片的一邊上,則∠1和∠2的關系是( )| A. | ∠1=∠2 | B. | ∠1+∠2=90° | C. | ∠1+∠2=180° | D. | 不能確定 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
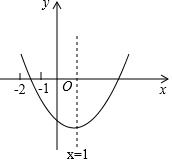 二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則$\frac{b}{a}$的值為-2;$\frac{c}{a}$的取值范圍為-8<$\frac{c}{a}$<-3.
二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則$\frac{b}{a}$的值為-2;$\frac{c}{a}$的取值范圍為-8<$\frac{c}{a}$<-3.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
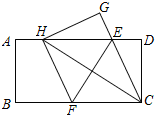 如圖,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將紙片ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,有以下四個結論:
如圖,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將紙片ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,有以下四個結論:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
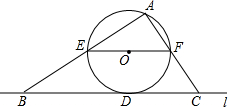 如圖,直線l與⊙相切于點D,過圓心O作EF∥l交⊙O于E、F兩點,點A是⊙O上一點,連接AE,AF,并分別延長交直線于B、C兩點;若⊙的半徑R=5,BD=12,則∠ACB的正切值為$\frac{7}{5}$.
如圖,直線l與⊙相切于點D,過圓心O作EF∥l交⊙O于E、F兩點,點A是⊙O上一點,連接AE,AF,并分別延長交直線于B、C兩點;若⊙的半徑R=5,BD=12,則∠ACB的正切值為$\frac{7}{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com