
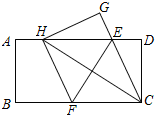
 如圖,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將紙片ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,有以下四個結論:
如圖,在一張矩形紙片ABCD中,AB=4,BC=8,點E,F分別在AD,BC上,將紙片ABCD沿直線EF折疊,點C落在AD上的一點H處,點D落在點G處,有以下四個結論:分析 ①先判斷出四邊形CFHE是平行四邊形,再根據翻折的性質可得CF=FH,然后根據鄰邊相等的平行四邊形是菱形證明,判斷出①正確;
②點H與點A重合時,設BF=x,表示出AF=FC=8-x,利用勾股定理列出方程求解得到BF的最小值,點G與點D重合時,CF=CD,求出BF=4,然后寫出BF的取值范圍,判斷出②正確;
③根據菱形的對角線平分一組對角線可得∠BCH=∠ECH,然后求出只有∠DCE=30°時EC平分∠DCH,判斷出③錯誤;
④過點F作FM⊥AD于M,求出ME,再利用勾股定理列式求解得到EF,判斷出④正確.
解答 解:①∵FH與EG,EH與CF都是原來矩形ABCD的對邊AD、BC的一部分,
∴FH∥CG,EH∥CF,
∴四邊形CFHE是平行四邊形,
由翻折的性質得,CF=FH,
∴四邊形CFHE是菱形,
故①正確;
②點H與點A重合時,設BF=x,則AF=FC=8-x,
在Rt△ABF中,AB2+BF2=AF2,
即42+x2=(8-x)2,
解得x=3,
點G與點D重合時,CF=CD=4,
∴BF=4,
∴線段BF的取值范圍為3≤BF≤4,
故②正確;
③∴∠BCH=∠ECH,
∴只有∠DCE=30°時EC平分∠DCH,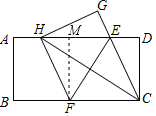 故③錯誤;
故③錯誤;
過點F作FM⊥AD于M,
則ME=(8-3)-3=2,
由勾股定理得,
EF=$\sqrt{M{F}^{2}+M{E}^{2}}$=2$\sqrt{5}$,
故④正確.
綜上所述,結論正確的有①②④.
故答案為:①②④.
點評 此題是四邊形綜合題,主要考查了折疊問題與菱形的判定與性質、勾股定理的綜合應用,熟練掌握菱形的判定定理和性質定理、勾股定理是解本題的關鍵.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優味美,客商聞訊前來采購,經協商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.
我市在黨中央實施“精準扶貧”政策的號召下,大力開展科技扶貧的惠農富農,老張在科技人員的指導下,改良柑橘品種,去年他家的柑橘喜獲豐收,而且質優味美,客商聞訊前來采購,經協商:采購價y(元/噸)與采購量x(噸)之間的函數關系如圖所示.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 6 | B. | 8 | C. | 9 | D. | 16 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com