
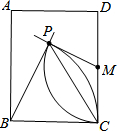
 如圖,長方形ABCD中,M為CD中點,分別以點B、M為圓心,以BC長、MC長為半徑畫弧,兩弧相交于點P.若∠PMC=110°,則∠BPC的度數為( )
如圖,長方形ABCD中,M為CD中點,分別以點B、M為圓心,以BC長、MC長為半徑畫弧,兩弧相交于點P.若∠PMC=110°,則∠BPC的度數為( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
分析 根據三角形內角和定理和等腰三角形兩底角相等求出∠MCP,然后求出∠BCP,再根據等腰三角形兩底角相等和三角形內角和定理求解即可.
解答 解:∵以B、M為圓心,分別以BC長、MC長為半徑的兩弧相交于P點,
∴BP=BC,MP=MC,
∵∠PMC=110°,
∴∠MCP=$\frac{1}{2}$(180°-∠PMC)=$\frac{1}{2}$(180°-110°)=35°,
在長方形ABCD中,∠BCD=90°,
∴∠BCP=90°-∠MCP=90°-35°=55°,
∴∠BCP=∠BPC=55°.
故選C.
點評 本題考查了矩形的四個角都是直角的性質,等腰三角形兩底角相等的性質以及等邊對等角,三角形內角和等于180°的知識點.


科目:初中數學 來源: 題型:填空題
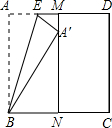 如圖,正方形紙片ABCD的邊長為1,M、N分別是AD、BC邊上的點,且AB∥MN,將紙片的一角沿過點B的直線折疊,使A落在MN上,落點記為A′,折痕交AD于點E,若M是AD邊上距D點最近的n等分點(n≥2,且n為整數),則A′N=$\frac{\sqrt{2n-1}}{n}$.
如圖,正方形紙片ABCD的邊長為1,M、N分別是AD、BC邊上的點,且AB∥MN,將紙片的一角沿過點B的直線折疊,使A落在MN上,落點記為A′,折痕交AD于點E,若M是AD邊上距D點最近的n等分點(n≥2,且n為整數),則A′N=$\frac{\sqrt{2n-1}}{n}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | (a2b)3=a6b3 | B. | a6÷a2=a3(a≠0) | C. | a-2=-$\frac{1}{{a}^{2}}$(a≠0) | D. | $\root{3}{(-2)^{3}}$=2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com