

分析 (1)設小亮從乙地到甲地過程中y2(米)與x(分鐘)之間的函數關系式為y2=k2x+b,由待定系數法根據圖象就可以求出解析式;
(2)先根據函數圖象求出甲乙的速度,然后與追擊問題就可以求出小亮追上小明的時間,就可以求出小亮從甲地返回到與小明相遇的過程中s(米)與x(分鐘)之間的函數關系式;
(3)先根據相遇問題建立方程就可以求出a值,10分鐘甲、乙走的路程就是相距的距離,14分鐘小明走的路程和小亮追到小明時的時間就可以補充完圖象.
解答 解:(1)設小亮從乙地到甲地過程中y2(米)與x(分鐘)之間的函數關系式為y2=k2x+b,由圖象,得
$\left\{\begin{array}{l}{2000=b}\\{0=10{k}_{2}+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-200}\\{b=2000}\end{array}\right.$,
∴y2=-200x+2000;
(2)由題意,得
小明的速度為:2000÷40=50米/分,
小亮的速度為:2000÷10=200米/分,
∴小亮從甲地追上小明的時間為(24×50)÷(200-50)=8分鐘,
∴24分鐘時兩人的距離為:S=24×50=1200,32分鐘時S=0,
設S與x之間的函數關系式為:S=kx+b1,由題意,得
$\left\{\begin{array}{l}{1200=24k+{b}_{1}}\\{0=32k+{b}_{1}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-150}\\{{b}_{1}=4800}\end{array}\right.$,
∴S=-150x+4800(24≤x≤32);
(3)由題意,得
a=2000÷(200+50)=8分鐘,
當x=24時,S=1200,
設經過x分鐘追上小明,則200x-50x=1200,解得x=8,此時的總時間就是24+8=32分鐘.
故描出相應的點就可以補全圖象.
如圖: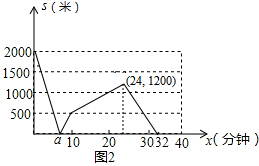
點評 本題考查了待定系數法求一次函數的解析式的運用,追擊問題與相遇問題在實際問題中的運用,描點法畫函數圖象的運用,解答時靈活運用路程、速度、時間之間的數量關系是關鍵.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,反比例函數y=$\frac{k}{x}$的圖象經過點A(1,4),B(m,n).
在平面直角坐標系xOy中,反比例函數y=$\frac{k}{x}$的圖象經過點A(1,4),B(m,n).查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
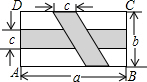 長方形ABCD中,橫向陰影部分是長方形,另一部分是平行四邊形,依照圖中標注的數據,圖中空白部分的面積是( )
長方形ABCD中,橫向陰影部分是長方形,另一部分是平行四邊形,依照圖中標注的數據,圖中空白部分的面積是( )| A. | bc-ab+ac+c2 | B. | ab-bc-ac+c2 | C. | a2+ab+bc-ac | D. | b2-bc+a2-ab |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
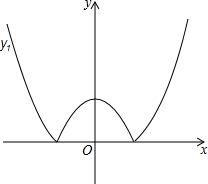 如圖,將二次函數y=x2-m(其中m>0)的圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,形成新的圖象記為y1,另有一次函數y=x+b的圖象記為y2,則以下說法:
如圖,將二次函數y=x2-m(其中m>0)的圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,形成新的圖象記為y1,另有一次函數y=x+b的圖象記為y2,則以下說法:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
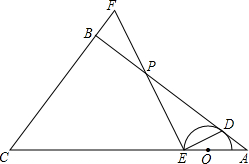 如圖,在△ABC中,∠ABC=90°,AB=4,BC=3,O是邊AC上的一個動點,以點O為圓心作半圓,與邊AB相切于點D,交線段OC于點E,連接ED,過點E作ED的高,交射線AB于點P,交射線CB于點F.
如圖,在△ABC中,∠ABC=90°,AB=4,BC=3,O是邊AC上的一個動點,以點O為圓心作半圓,與邊AB相切于點D,交線段OC于點E,連接ED,過點E作ED的高,交射線AB于點P,交射線CB于點F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com