
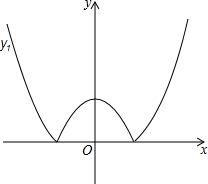
 如圖,將二次函數(shù)y=x2-m(其中m>0)的圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,形成新的圖象記為y1,另有一次函數(shù)y=x+b的圖象記為y2,則以下說法:
如圖,將二次函數(shù)y=x2-m(其中m>0)的圖象在x軸下方的部分沿x軸翻折,圖象的其余部分保持不變,形成新的圖象記為y1,另有一次函數(shù)y=x+b的圖象記為y2,則以下說法:分析 ①錯誤.如圖1中,當(dāng)直線y=x+b與拋物線相切時,也滿足條件只有三個交點.此時b≠1,故①錯誤.
②正確.如圖2中,當(dāng)拋物線經(jīng)過點(-2,0)時,0=4-m,m=4,觀察圖象可知m>4時,y1與y2恰有兩個交點.
③錯誤.如圖3中,當(dāng)b=-4時,觀察圖象可知,y1與y2沒有交點,故③錯誤.
④正確.如圖4中,當(dāng)b=4時,觀察圖象可知,b>0,y1與y2至少有2個交點,且其中一個為(0,b),故④正確.
解答 解:①錯誤.如圖1中,當(dāng)直線y=x+b與拋物線相切時,也滿足條件只有三個交點.此時b≠1,故①錯誤.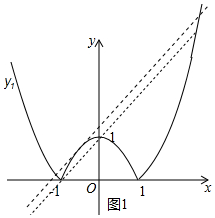
②正確.如圖2中,當(dāng)拋物線經(jīng)過點(-2,0)時,0=4-m,m=4,觀察圖象可知m>4時,y1與y2恰有兩個交點.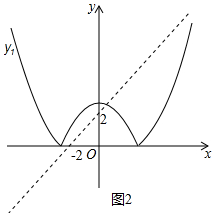
由$\left\{\begin{array}{l}{y=x+2}\\{y=-{x}^{2}+m}\end{array}\right.$消去y得到x2+x+2-m=0,當(dāng)△=0時,1-8+4m=0,
∴m=$\frac{7}{4}$,
觀察圖象可知當(dāng)0<m<$\frac{7}{4}$時,y1與y2恰有兩個交點.故②正確.
③錯誤.如圖3中,當(dāng)b=-4時,觀察圖象可知,y1與y2沒有交點,故③錯誤.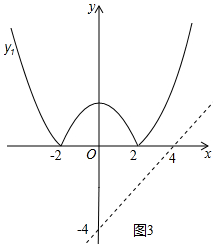
④正確.如圖4中,當(dāng)b=4時,觀察圖象可知,b>0,y1與y2至少有2個交點,且其中一個為(0,b),故④正確.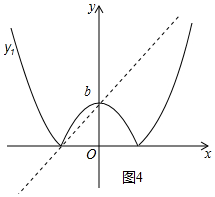
故答案為②④
點評 本題考查二次函數(shù)與x軸的交點、一次函數(shù)的應(yīng)用、函數(shù)與方程的關(guān)系等知識,解題的關(guān)鍵是學(xué)會利用函數(shù)圖象解決問題,學(xué)會利用根的判別式解決函數(shù)圖象的交點問題,屬于中考常考題型.


科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖所示,已知點E是四邊形ABCD內(nèi)的一點,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,試說明AD與BC的位置關(guān)系.
如圖所示,已知點E是四邊形ABCD內(nèi)的一點,若AE平分∠BAD,BE平分∠ABC,且∠1+∠2=90°,試說明AD與BC的位置關(guān)系.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com