Question

13．已知四邊形ABCD中，AB=BC，∠ABC=90°，AD∥BC，E為CD上一點，且AE=AB，∠BAE=60°
（1）如圖1，①求∠AED的度數(shù)；
②求證：DE=CE；
（2）如圖2，過E作EF⊥CD交AB于點F，若$\frac{BF}{AF}$=$\frac{1}{2}$，求$\frac{AD}{BC}$的值．

Answer 1

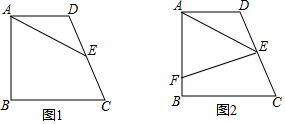
分析 （1）①連接BE，作EH⊥AB于H，根據(jù)題意得到△ABE是等邊三角形，根據(jù)等腰三角形的性質得到∠AEH=30°，∠BEC=∠C=75°，計算即可；
②根據(jù)平行線分線段成比例定理證明即可；
（2）作AG⊥AE交EF的延長線于G，證明△AFG≌△ADE，得到AF=AD，根據(jù)題意計算即可．

解答 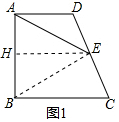解：（1）①如圖1，連接BE，作EH⊥AB于H，
∵AE=AB，∠BAE=60°，
∴△ABE是等邊三角形，
∴∠AEB=∠ABE=60°，
∵EH⊥AB，
∴∠AEH=30°，
∵∠ABC=90°，∠ABE=60°，
∴∠EBC=30°，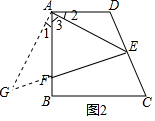
∵BE=BC，
∴∠BEC=∠C=75°，
∴∠AED=180°-75°-60°=45°；
②∵EH⊥AB，∠ABC=90°，AD∥BC，
∴AD∥BC∥EH，又AH=HB，
∴DE=CE；
（2）如圖2，作AG⊥AE交EF的延長線于G，
∵EF⊥CD，∠AED=45°，
∴∠AEG=45°，
∴∠AGE=45°，
∴AG=AE，
∵∠GEF=∠BAD=90°，
∴∠1+∠3=∠2+∠3=90°，
∴∠1=∠2，
在△AFG和△ADE中，
$\left\{\begin{array}{l}{∠1=∠2}\\{AG=AE}\\{∠AGE=∠AED}\end{array}\right.$，
∴△AFG≌△ADE，
∴AF=AD，
∵$\frac{BF}{AF}$=$\frac{1}{2}$，
∴$\frac{AF}{AB}$=$\frac{2}{3}$，
∴$\frac{AD}{BC}$=$\frac{2}{3}$．

點評 本題考查的是相似三角形的性質，掌握相似三角形的判定定理和性質定理、等邊三角形的判定定理和性質定理、等腰三角形的性質是解題的關鍵．