
| 港口 | 運費(元/噸) | |
| 甲庫 | 乙?guī)?/TD> | |
| A港 | 14 | 20 |
| B港 | 10 | 8 |
| 港口 | 運費(元/噸) | |
| 甲庫 | 乙?guī)?/TD> | |
| A港 | x | 100-x |
| B港 | 80-x | x-30 |
分析 (1)設從甲倉庫運送到A港口的物資為x噸,因為甲倉庫一共有物資80噸,所以甲倉庫運送到B港口的物資為(80-x)噸,因為A港口需要運送100噸物資,所以還要從乙倉庫運送到A港口的物資為(100-x)噸,又因為乙倉庫存有70噸物資,所以余下的物資:70-(100-x)=(x-30)噸,都要運到B港口;
(2)總費用=物資數(shù)量×運費,化成一般式即可,將甲、乙兩倉庫運往A、B兩港口的物資數(shù)分別大于等于0,列不等式可求其x的取值范圍;
(3)根據(jù)一次函數(shù)的增減性求得最小值,并寫出調(diào)配方案.
解答 解:(1)設從甲倉庫運送到A港口的物資為x噸,則甲倉庫運送到B港口的物資為(80-x)噸,乙倉庫運送到A港口的物資為(100-x)噸,乙倉庫運送到B港口的物資為70-(100-x)=(x-30)噸,
故答案為:100-x,80-x,x-30;
(2)y=14x+10(80-x)+20(100-x)+8(x-30)=-8x+2560,
由題意得:$\left\{\begin{array}{l}{x≥0}\\{80-x≥0}\\{100-x≥0}\\{x-30≥0}\end{array}\right.$,
∴不等式的解集為:30≤x≤80,
∴總費用y(元)與x(箱)之間的函數(shù)關(guān)系式為:y=-8x+2560(30≤x≤80);
(3)∵-8<0,
∴y隨x的增大而減小,
∴當x=80時,y有最小值,y=-8×80+2560=1920,
答:最低費用為1920元,此時的調(diào)配方案為:把甲倉庫的全部運往A港口,再從乙倉庫運20噸到A港口,乙倉庫余下的50噸全部分運往B港口.
點評 本題是一次函數(shù)的應用,屬于運輸方案問題,此類問題比較麻煩,要認真理順兩倉庫運往兩地的物資數(shù)和運費;熟練掌握一次函數(shù)的增減性的性質(zhì),根據(jù)實際問題中的取值確定其最大值和最小值.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數(shù)學 來源: 題型:選擇題
| A. | (5,4) | B. | (-5,-4) | C. | (-3,-4) | D. | (-5,4) |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
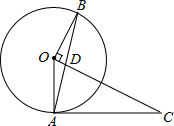 如圖,在△OAC中,以點O為圓心、OA長為半徑作⊙O,作OB⊥OC交⊙O于點B,連接AB交OC于點D,∠CAD=∠CDA.
如圖,在△OAC中,以點O為圓心、OA長為半徑作⊙O,作OB⊥OC交⊙O于點B,連接AB交OC于點D,∠CAD=∠CDA.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com