
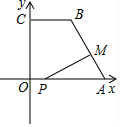
 如圖,在平面直角坐標(biāo)系中,已知點A(10,0),B(4,8),C(0,8),連接AB,BC,點P在x軸上,從原點O出發(fā),以每秒1個單位長度的速度向點A運動,同時點M從點A出發(fā),以每秒2個單位長度的速度沿折線A-B-C向點C運動,其中一點到達終點時,另一點也隨之停止運動,設(shè)P,M兩點運動的時間為t秒.
如圖,在平面直角坐標(biāo)系中,已知點A(10,0),B(4,8),C(0,8),連接AB,BC,點P在x軸上,從原點O出發(fā),以每秒1個單位長度的速度向點A運動,同時點M從點A出發(fā),以每秒2個單位長度的速度沿折線A-B-C向點C運動,其中一點到達終點時,另一點也隨之停止運動,設(shè)P,M兩點運動的時間為t秒.分析 (1)過點B作BD⊥x軸于點D,利用勾股定理求出AB的長度;
(2)先判斷出點M在AB上,然后表示出PA,ME即可用三角形的面積公式即可;
(3)△APM為直角三角形時,由于沒有規(guī)定哪個頂點是直角頂點,所以分三種情況進行討論;利用銳角三角函數(shù)或相似三角形的性質(zhì)即可.
解答 解:(1)如圖1, 過點B作BD⊥x軸于點D,
過點B作BD⊥x軸于點D,
∵A(10,0),B(4,8)C(0,8),
∴AO=10,BD=8,AD=6,
由勾股定理可求得:AB=10,
(2)∵AB=10,
∴10÷2=5,
∵0≤t≤5,
∴點M在AB上,
作ME⊥OA于E,
∴△AEM∽△ADB,
∴$\frac{ME}{BD}=\frac{AM}{AB}$,
∴$\frac{ME}{8}=\frac{2t}{10}$,
∴ME=$\frac{8}{5}$t,
∴S=$\frac{1}{2}$PA•ME=$\frac{1}{2}$(10-t)$•\frac{8}{5}t$=-$\frac{4}{5}{t}^{2}+8t$=-$\frac{4}{5}$(t-5)2+20,
∵0≤t≤5,
∴t=5時,S取最大值,此時PA=10-t=5,
即:點P在OA的中點處.
(3)由題意可知:0≤t≤7,
當(dāng)點P是直角頂點時,
∴PM⊥AP,
∴PA=10-t,
若0≤t≤5時,點M在AB上,如圖2,
此時AM=2t,
∵cos∠BAO=$\frac{3}{5}$,
∴$\frac{AP}{AM}$=$\frac{3}{5}$,
∴$\frac{10-t}{2t}=\frac{3}{5}$
∴t=$\frac{50}{11}$,
若5<t≤7時,點M在BC上,如圖3,
∴CM=14-2t,OP=t,
∴OP=CM,
∴t=14-2t,
∴t=$\frac{14}{3}$,
當(dāng)點A是直角頂點時,
此時,∠MAP不可能為90°,此情況不符合題意;
當(dāng)點M是直角頂點時,
若0≤t≤5時,M在AB上,如圖4,
此時,AM=2t,AP=10-t
∵cos∠BAO=$\frac{3}{5}$,
∴$\frac{AM}{AP}=\frac{3}{5}$,
∴$\frac{2t}{10-t}=\frac{3}{5}$,
∴t=$\frac{30}{13}$,
若5<t≤7時,點M在BC上,如圖5,
過點M作ME⊥x軸于點E,
此時,CM=14-2t,OP=t,
∴ME=8,PE=CM-OP=14-3t,
∴EA=10-(14-2t)=2t-4,
∵∠PMA=∠MEA=90°,
∴∠PME+∠EMA=∠EMA+∠MAP=90°,
∴∠PME=∠MAP,
∴△PME∽△MAE,
∴$\frac{ME}{PE}=\frac{EA}{ME}$,
∴ME2=PE•EA,
∴64=(14-3t)(2t-4),
∴3t2-8t+60=0,
△=-656<0,故此情況不存在;
綜上所述,t=$\frac{50}{11}$或$\frac{30}{13}$;
點評 此題是三角形的綜合問題,涉及平行四邊形的判定與性質(zhì),相似三角形的判定與性質(zhì),銳角三角函數(shù),三角形的面積公式,解方程等知識,畫出圖形是解本題的關(guān)鍵,綜合程度較高.


 小天才課時作業(yè)系列答案
小天才課時作業(yè)系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導(dǎo)學(xué)系列答案
新輔教導(dǎo)學(xué)系列答案 陽光同學(xué)一線名師全優(yōu)好卷系列答案
陽光同學(xué)一線名師全優(yōu)好卷系列答案科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,矩形OABC的頂點A,C分別在x軸和y軸上,點B的坐標(biāo)為(4,6).雙曲線y=$\frac{k}{x}$(x>0)的圖象經(jīng)過BC的中點D,且與AB交于點E,連接DE.
如圖,矩形OABC的頂點A,C分別在x軸和y軸上,點B的坐標(biāo)為(4,6).雙曲線y=$\frac{k}{x}$(x>0)的圖象經(jīng)過BC的中點D,且與AB交于點E,連接DE.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 1500米 | B. | 1575米 | C. | 2000米 | D. | 2075米 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
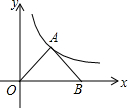 已知,如圖所示,在平面直角坐標(biāo)系中,Rt△OAB的直角頂點A在反比例函數(shù)y=$\frac{4\sqrt{3}}{x}$(x>0)圖象上,∠AOB=30°,頂點B在x軸上,求此△OAB頂點A的坐標(biāo)和△OAB面積.
已知,如圖所示,在平面直角坐標(biāo)系中,Rt△OAB的直角頂點A在反比例函數(shù)y=$\frac{4\sqrt{3}}{x}$(x>0)圖象上,∠AOB=30°,頂點B在x軸上,求此△OAB頂點A的坐標(biāo)和△OAB面積.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
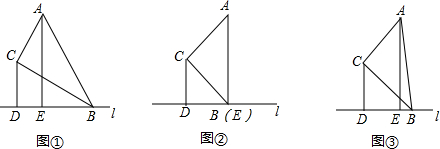
 如圖,在△ABC中,∠ACB=90°,AC=BC,E為AC邊的中點,過點A作AD⊥AB交BE的延長線于點D,CG平分∠ACB交BD于點G,F(xiàn)為AB邊上一點,連接CF,且∠ACF=∠CBG.
如圖,在△ABC中,∠ACB=90°,AC=BC,E為AC邊的中點,過點A作AD⊥AB交BE的延長線于點D,CG平分∠ACB交BD于點G,F(xiàn)為AB邊上一點,連接CF,且∠ACF=∠CBG.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com